ここでは、因数分解を学ぼう。

因数分解とは

ここでは、因数分解（いんすうぶんかい）を学ぼう。
因数分解ってなんだろう？
因数分解は、整数や多項式を、簡単な項のかけ算に書きかえることなんだ。

整数を因数分解すると、素数のかけ算にできるんだ。
文字を含む多項式を因数分解すると、単項式や多項式のかけ算にできるんだ。

整数の因数分解

整数を因数分解してみよう。
はじめに、６を因数分解してみよう。
因数分解は、素数のかけ算にするんだったね。
６をかけ算に書きかえると、

の２つがあるね。
かけ算は順番を変えても計算の結果は同じだから、どっちを書いてもいいんだ。
だけど、かけ算する整数の数が多くなってくると、分かりにくくなるよね。
だから、数の大きい順か小さい順に書くのがいいよ。

たとえば、

よりも、
か、
の方が、数が順番に並んでいるので見やすいよね。
答えがあっているのは大切だけど、同じ正解だったら、より美しい正解の方がカッコいいよね。

整数の因数分解はどうやってするの？

整数の因数分解はどうやってするんだろう？
整数をかけ算にする方法は以前に学んだよね。
わり算？ではなくて、「最大公約数」や「最小公倍数」を考えるときに使った、「素因数分解」を使うんだ。
「素因数分解」はこちらで確認しよう。

では、２４を因数分解してみよう。
筆算（ひっさん）を書くと、

になるね。
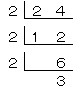
だから、２４を因数分解すると、
だね。
乗数をつかってカッコよく書くと、
だね。

多項式の因数分解

多項式を因数分解してみよう。
はじめに、数字だけの多項式を因数分解してみよう。
下記の多項式を因数分解してみよう。

さて、どうやって因数分解しよう。
多項式を計算してから、素因数分解すると因数分解できるよね。
多項式を計算すると、
だね。これを素因数分解の筆算をすると、
になるね。
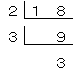
だから、「２×３＋２×６」を因数分解すると、
だね。

答えは合っているけど、、、
多項式のかけ算とたし算を計算したのに、因数分解して、もう一度かけ算の式にしているから、なんかムダな計算をしたような気がするね。
多項式のかけ算をせずに、因数分解できないかな？　考えてみよう。

それでは、数字を使って考えてみよう。
「２×３＋２×６」をたし算を使って書きかえると、
２が３コあるたし算と、２が６コあるたし算だよね。
つまり、

だよね。
これを、かけ算に書き換えると、２が（３＋６）コだから、
だよね。

上の式に、とても重要な式が含まれているから、抜き出してみるよ。

これは、「分配法則」というんだ。
重要な法則だから覚えておこう。
なぜこの法則が成り立つかは、さっき上で考えたよね。
「２」を３コと「２」を６コを足した数は、「２」を９コ（３コ＋６コ）足した数と同じになるんだったよね。

では、次の問題を考えてみよう。
下の式を計算するといくつになるか。

どうやって計算しよう。
そうだね、両方の項に「８」が含まれているよね。
分配法則を使って考えると、
だね。

因数分解すると、

だね。

文字のある多項式の因数分解

つぎに、文字を含んでいる多項式を因数分解してみよう。
さっきは数字だけの多項式を因数分解したから、素数の掛け算になったね。
では、文字を含む式の因数分解をすると、どんな式になるといいのかな？
そうだね、簡単な式の掛け算になればいいんだよね。
「因数分解」は「展開」と逆のことをするんだ。
では、下記の多項式を因数分解してみよう。

さて、どうやって因数分解しよう。

「因数分解」は「展開」と逆のことをするんだったね。
だから、まずは全部の項に含まれている、共通の項を探し出すんだ。
そしてその共通の項の掛け算にすればいいよね。

まずはやってみよう。
全部の項、２x２とx、に含まれている項は何かな？
そうだね、xが含まれているね。
だから、xの掛け算にすればいいよね。
xの掛け算に書き変えると、

xの掛け算にすると、
だね。
文字を含む式では×を省略して書くことが多いから、×を省略して書くと、
だね。
これよりも簡単な式にはならないから、答えは、
だね。
「（２x＋１）」を「２（x＋）」に書き換えられるって？
そうだね、xは簡単な式になったけど、分数のは簡単な式じゃないよね。だから差し引きすると同じくらいの簡単さかな。
２の掛け算にしてもいいけど、簡単さは変わらないし、計算の回数も増えるから、２の掛け算にはしないことが多いみたいだよ。