ここでは、「公倍数（こうばいすう）」を説明するよ。

「倍数」ってなぁに？

「倍数」って漢字が並んでて、難しそうだね。
でも、難しそうに見えるだけだから、楽しく考えよう。

はじめに、「倍数」について考えよう。
「倍数」ってなんだろう？

生活している中で、

とかって言わない？

この元の量を「２倍」や「４倍」した量が「倍数」なんだ。
別の言い方をすると、ある数を２倍、３倍、４倍・・・と倍にした数の集まりが倍数なんだ。

もとの数が「２」とすると、
２，４，６，８，１０，・・・・ なんだ。

もとの数が「３」とすると、倍数は、
３，６，９，１２，１５，・・・・ なんだ。

あっ、倍数の一番小さな数は、もとの数と同じだね。
倍数は「もとの数」が分かると、ほかの数が計算できるから、「もとの数」がとても大事なんだ。
そこで、「もとの数」が２のときの倍数を「２の倍数」、もとの数が４のときの倍数を「４の倍数」っていうように、もとの数が●●のときは「●●の倍数」っていうんだ。

次の問題を考えてみよう。

さあ、考えよう。

一番小さな７の倍数は、もとの数と同じだから、７だよね。
次に小さな数は、７の２倍だから、１４。
その次に小さな数は、７の３倍だから、２１。
この順番で考えると、答えは、
だね。

次の問題を考えてみよう。

さあ、考えよう。

倍数はどんどん数が大きくなるけど、質問には「６０より小さい数」って書いているよ。
７の倍数で６０より小さくて、一番大きな数はなんだろう？
・・・そうだ！　７の倍数を書いてみよう。
このなかで、６０より小さいのは、
だね。
だから、答えは、
だね。

・・・答えは合っているけど、もし問題文が、
だったらどうしよう？
７，１４，２１・・・と書いていくのは大変だよ。それになんといっても、カッコいい考え方じゃないよね。

どうしよう・・・。
そうだね、７の倍数っていうことは、７で割り切れるってことだよね。
６０を７で割ると、
だよね。
図で書くと、こんな感じかな。



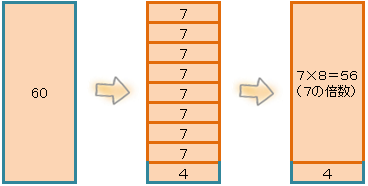
７が８つあるよね。７×８は７の倍数だよね。
だから、７の倍数で、６０より小さい一番大きな数は、７×８だね。これを計算すると、
だね。だから、答えは、
だね。


さあ、これで、
をカッコよく計算できるね。

を計算すると、
だね。
だから、７の倍数で、１００より小さい一番大きな数は、７×１４だね。
これを計算すると、
だね。だから答えは、
だね。

公倍数・最小公倍数

さっきは「倍数」を考えたね。
ここでは、「公倍数（こうばいすう）」と「最小（さいしょう）公倍数」を考えよう。


「公」の意味は「全体」っていうだけあって、「公倍数」は２つ以上の数のときに計算できるんだ。
２つ以上の「もとの数」の、それぞれの倍数の中から、同じ倍数だけを集めたものが「公倍数」なんだ。

言葉ではわかりにくいから、次の問題を見てみよう。
さあ、考えよう。

はじめに、２の倍数と、３の倍数を考えてみよう。

２と３の公倍数は、２の倍数にも、３の倍数にも含まれる倍数だから、２の倍数と、３の倍数を比べて、同じ倍数を考えてみよう。
だね。だから、答えは、
だね。
これをみて気が付いたかな？
公倍数は、６の倍数になっているね。
公倍数は、一番小さな公倍数の倍数になっているんだ。
一番小さな公倍数を、最小（さいしょう）公倍数っていうんだ。

公倍数の中で、一番小さな公倍数を、最小（さいしょう）公倍数というんだ。
最小公倍数は、「分数」の計算でも使うから、マスターしておこう。

では、次の問題を考えよう。
２と３の公倍数は、６，１２，１８，・・・だから、最小公倍数は６だね。
だから答えは、
だね。
公倍数が分かっていると、最小公倍数は簡単に分かるね。

次は「公倍数」をカッコよく計算する方法を考えよう。
その前に、「公倍数」によく似ている、「公約数」について学ぼう。

「公約数」のページはココをクリック。