ここでは、「公倍数(こうばいすう)」と「公約数(こうやくすう)」を計算で導き出す方法を説明するよ。
「素因数分解(そいんすうぶんかい)」ってなに?
公倍数と公約数の考え方は分かったけど、カッコよく計算する方法はないのかな?
「2と3の公倍数」を見つけるために、「2の倍数」と「3の倍数」をたくさん書いて探すのは大変だよね。
「12と15の公約数」を見つけるために、「12の約数と15の約数」を全部書いて探すのは大変だよね。
そのためには、素因数分解(そいんすうぶんかい)を使うと便利なんだ。
カッコいい計算のやり方だから、覚えよう。
素因数分解には「素数」を使うよ。「素数」をわすれたら、こちらで確認しよう。
次の問題を考えてみよう。
6を素数のかけ算にするのだから、6が何で割り切れるかを考えればいいよね。
割り切れる数は、約数だよね。
2)6=2×3
3)6=3×2
4)6=6×1
1)と4)は、もとの数字の6がまだあるから、6を書き換えていないよね。。。
2)と3)は、使っている数字が2と3で同じだね。かけ算は、数字の順番を入れ替えても答えは同じだったよね。
だから、2)と3)は答えが同じになるから、どちらを書いてもいいんだ。
ここからは、2)の式を使って考えよう。
3は素数かな? 素数だよね。
だから、答えは、
実は今、6を素因数分解したんだよ。
もとの数を、素数だけのかけ算にすることを「素因数分解」というんだ。
もとの数を、素数で書き換えるのって、カッコいいよね。
素因数分解の仕方を覚えよう。
次の問題を考えてみよう。
24の約数は、1,2,3,4,6,8,12,24だよね。
いろんな数で割り切れるね。素数じゃない数も含まれているね。
24を簡単に素数のかけ算に書き換えられないかな?
素因数分解は、もとの数を素数だけのかけ算に書き換えるんだよね。
だから、もとの数を、素数でわり算して、もとの数に含まれている素数を計算しよう。
はじめに、もとの数の24を、素数の2で割ろう。
=2×2×6
=2×2×2×3
さて、24を素因数分解するときに、何回もわり算をしたよね。
24を2でわり算するとき、ひっ算は、
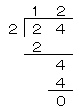
でも、これだと、次に12を2でわり算するときに、別にひっ算を書かないといけないから、分かりにくいよね。
実は、素因数分解がしやすいひっ算の書き方があるんだ。
それは、24を2でわり算するときは、
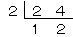
わり算の答えの12は、24の下に書くんだ。
わり算のひっ算と同じように、十の桁と、一の桁は縦にならぶように書くんだ。
次に12を2で割り算するよ。このときは、
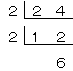
次に6を2で割り算するよ。このときは、
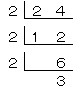
ここで、左の数字と、一番下の数字をかけ算してみよう。
下のオレンジ色の数字だよ。
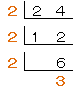
これは、24の素因数分解した式なんだ。
だから、24を素因数分解した式は、
公倍数を計算する
次の問題を考えてみよう。
4と6の二つがあるから、4と6を別々に考えよう。
はじめに、4の倍数を考えてみよう。
4を素因数分解のひっ算をすると、
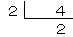
4の倍数を、2×2を使って書くと、
4×2=2×2×2=8
4×3=2×2×3=12
これからわかるように、4の倍数は、必ず2が二つあるんだ。
それはそうだよね。
だって、4=2×2、だから、2が二つあるよね。
でも、これはとても大事なことなんだ。
つぎに、6の倍数を考えてみよう。
6を素因数分解のひっ算をすると、
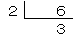
6の倍数を、2×3(または3×2)を使って書くと、
6×2=2×3×2=12
6×3=2×3×3=18
これからわかるように、6の倍数は、必ず2が一つと、3が一つあるんだ。
それはそうだよね。
だって、6=2×3、だから、2が一つと、3が一つあるよね。
でも、これはとても大事なことなんだ。
さて、4と6の公倍数は、4の倍数であり、6の倍数だから、
6の倍数になるための、2×3がある
これを考えると、4と6の公倍数は、
この式を計算すると、
だから、次の問題の答えは、
12×2=24
12×3=36
ちなみに、最小公倍数は、一番小さな公倍数だから、12、だよね。
最小公倍数を計算する
最小公倍数の計算は、公倍数の計算と同じだね。
つぎの問題を考えよう。
8を素因数分解すると、
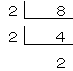
[式]
8=2×2×2
だから、8の倍数は2が三つあるんだ。
12を素因数分解すると、
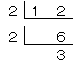
[式]
12=2×2×3
だから、12の倍数は2が二つと、3が一つあるんだ。
だから、8と12の最小公倍数は、
12の倍数:2×2×3
こうすると、8の倍数の2×2×2を持っているし、
これを計算すると、
公約数と最大公約数を計算する
次の問題を考えてみよう。
また、最大公約数を答えよ。
考える数が24と42の二つがあるから、別々に考えよう。
はじめに、24の約数を考えてみよう。
24を素因数分解すると、
約数は、もとの数をちょうど割り切れる数だから、
たとえば、2は約数だね。
なぜなら、計算すると、
わり算とかけ算は順番を入れ替えることができるから、
24÷2=2÷2×2×2×3
=1×2×2×3
=2×2×3
実は、24を素因数分解した数(2が三つと、3が一つ)を使って計算できる数が、約数なんだ。
たとえば、2を二つと3を一つ使った数(2×2×3)は24の約数なんだ。
ためしに、計算してみよう。
=2×2×2×3÷2÷2÷3
=2÷2×2÷2×2×3÷3
=1×1×2×1
=2
だから、24の約数は1を含めて書くと、下記の数になるんだ。
2
2×2=4
2×2×2=8
3
3×2=6
3×2×2=12
3×2×2×2=24
2
3
2×2=4
3×2=6
2×2×2=8
3×2×2=12
3×2×2×2=24
つぎに、42の約数を考えてみよう。
42を素因数分解すると、
だから、約数を小さい順に書くと、
2
3
3×2=6
7
7×2=14
7×3=21
7×2×3=42
24と42の公約数は、24を割っても、42を割っても、割り切れる数だね。
だから、公約数は、24の素因数に含まれていなければならないし、42の素因数に含まれていなければならないんだ。
つまり、公約数は、
42の素因数の、2×3×7、に含まれている
両方に含まれているのは、2が一つと、3が一つだね。
だから、公約数は、2を一つと、3を一つ使ってできるすべての数なんだ。
つまり、24と42の公約数は、1を含めると、
2
3
3×2=6
たしかにどの数も、24と42の素因数に含まれているよ。
だから、
また、最大公約数を答えよ。
最大公約数は、一番大きな公約数だから、