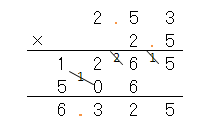ここでは、「小数」のかけ算とわり算を説明するよ。

「小数」のかけ算

小数のたし算とひき算は、整数のたし算とひき算と同じようにできたね。
次に、小数のかけ算を考えてみよう。
小数のかけ算も整数のかけ算と同じようにできるのかな？

まずは整数のかけ算の復習をしよう。下の問題を考えてみよう。

さあ、考えよう。
まずは図を描いてみよう。図を描くとこんな感じかな。

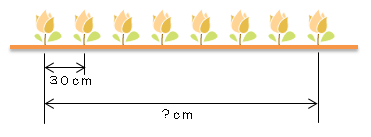
左端の花から右端の花までの距離は、
かな？
違うよね。
たとえば、花が２本のときは、左端から右端の花まで３０ｃｍだよね。
花が３本のときは、左端から右端の花まで６０ｃｍだよね。
つまり、
だね。

だから、式を書くと、
答えは、
だね。

次に下の問題を考えてみよう。

さあ、考えよう。
まずは図を描いてみよう。図を描くとこんな感じかな。

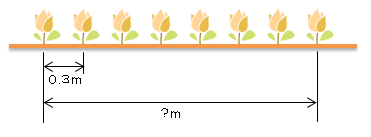
左端の花から右端の花までの距離は、
だね。
だから、式を書くと、

あ、小数と整数のかけ算だよ。
「０．３×７」はいくつかな。

「０．３×７」は０．３を７つ足した数のことだよね。
だから、たし算で書きかえると、「０．３×７」は、「０．３＋０．３＋０．３＋０．３＋０．３＋０．３＋０．３」と同じ大きさだよね。
「０．３＋０．３＋０．３＋０．３＋０．３＋０．３＋０．３」を計算すると、

になるね。
答えは合っているけど、たし算するのは大変だよね。
もっと簡単に計算できないかな？

「０．３×７＝２．１」をもっと簡単に計算する方法を考えよう。
はじめに、下の問題を考えてみよう。

１）の答えは、１０だよね。１００を１０等分したときの一つ分の大きさ、だからね。

２）の答えは、１だよね。１０を１０等分したときの一つ分の大きさ、だからね。

３）の答えは？
１を１０等分したときの一つ分の大きさは、０．１だよね。
だから、答えは、０．１だね。

４）の答えは？
０．１を１０等分したときの一つ分の大きさは、０．０１だよね。
だから、答えは、０．０１だね。

５）の答えは？
１）２）３）４）の答えを見てみると、ある数を１０で割ると、位が一つ小さくなっているよね。
だから、０．０１÷１０＝０．００１、になるね。

さっきも書いたけれど、ある数を１０で割ると位が一つ小さくなるんだ。
これは大事なことだから覚えておこう。

次に、下の問題を考えてみよう。

１）の答えは、１０００だよね。１００が１０集まると、位が上がるからね。

２）の答えは、１００だよね。１０が１０集まると、位が上がるからね。

３）の答えは、１０だよね。１が１０集まると、位が上がるからね。

４）の答えは？
０．１は１を１０等分した大きさだよね。その０．１が１０集まると、もとの１の大きさになるよね。
だから、答えは、

だね。

５）の答えは？
０．０１は０．１を１０等分した大きさだよね。その０．０１が１０集まると、もとの０．１の大きさになるよね。
だから、答えは、

だね。

１）～５）を見てみると、１０を掛けると位が一つ大きくなることが分かるね。
これは大事なことだから覚えておこう。

それじゃあ、「０．３×７＝２．１」をもっと簡単に計算する方法をもう一度考えよう。
１０で割ると位が一つ小さくなり、１０を掛けると位が一つ大きくなるんだよね。
それを使って、式を書きかえてみよう。
「０．３」は「３」を「１０」で割った数だよね。
なぜなら、「３」を「１０」で割ると位が一つ小さくなって、「０．３」になるからね。

に書きかえられるよね。
かけ算とわり算は計算の順番を変えても答えは変わらないから、「×７」を先に計算すると、
１０で割ると桁が一つ小さくなるから、
になるね。だから、答えは、
だね。
「０．３＋０．３＋０．３＋０．３＋０．３＋０．３＋０．３」を計算しなくても、かけ算を使って答えが計算できたね。

下の問題の答えは、０．３を７回たし算してもいいけど、かけ算を使ってカッコよく答えよう。

だね。

「小数」のかけ算のひっ算

整数のかけ算のひっ算を学んだよね。ひっ算を使うと計算がとても簡単に早くできたね。
どうやってするのか思い出せないときは、かけ算のひっ算を思い出そう。

小数のかけ算のひっ算はどうやってするのかな？
整数のかけ算のひっ算とはどこが違うのかな？
一緒に学んでいこう。

さっき「小数」のかけ算で解いた、

をひっ算で計算してみよう。

では、一つづつ順番に、ひっ算を書いていこう。
まず、かけ算の左側の数「０．３」を書くんだ。

次に、かけ算のひっ算だから、かけ算の記号「×」を下の行の左端（はし）に書くんだ。
次に、「０．３」の下にかけ算の右側の数「７」を書くんだ。
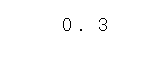
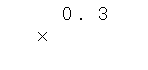
このとき、上の数と下の数の、右端をそろえて書くんだ。
右端の「３」と「７」をきちんとそろえて書こう。
次に、一番下に横線を書くんだ。

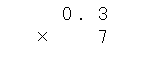
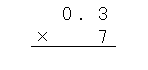
これで計算する準備が終わったよ。
整数のかけ算と同じだね。
さあ、つぎは、計算しよう。

まず、上の数の右端の数「３」と、下の数「７」をかけ算するんだよね。答えは「２１」だね。
上の数は十の位だから、十の位に「２」を書くんだよね。
繰り上がった数は、左上に小さく書くんだったね。

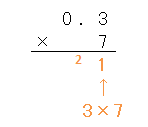
さあ、これでひっ算は終わったよ。
答えを見てみよう。

答えは、「２１」、かな？
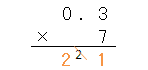
「３×７＝２１」だけど、「０．３×７」も２１なのかな？
かけ算している数が「３」と「０．３」で違っているから答えも違うはずだよね。
なにを忘れているのかな？
そうだね。小数点を考えるのを忘れていたね。
「０．３」の小数点はどこにつければいいのかな？

計算した結果に小数点を書こう。
小数点を書く位置はひっ算の式からわかるよ。

小数点の右端からの位置と同じ位置に、小数点をつけるだけなんだ。
「０．３」の小数点は右端から１つ目、「７」には小数点がないから０。 場所を足し算すると、

だから、「２１」の右端から１つ目に小数点をつけるんだ。
だからひっ算は、
になるから、答えは、
だね。
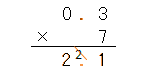
さっき計算した答えと同じになったね。

次は、

をひっ算で計算してみよう。

はじめにひっ算を書こう。
まず、かけ算の左側の数「２．５３」を書くんだったよね。

次に、かけ算のひっ算だから、かけ算の記号「×」を下の行の左端（はし）に書いて、「２．５３」の下に、かけ算の右側の数「２．５」を書くんだったよね。
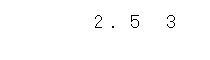
このとき、上の数と下の数の右端をそろえて書くんだったね。
右端の「３」と「５」をきちんとそろえて書こう。

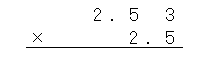
これで計算する準備が終わったよ。
さあ、計算しよう。

計算のしかたは整数のひっ算と同じだったね。
まず、上の数の右端の数「３」と、下の数の右端の数「５」をかけ算するんだよね。答えは「１５」だね。

つぎに、上の数の右端から二つ目の数「５」と、下の数の右端の数「５」をかけ算するんだよね。答えは「２５」だね。
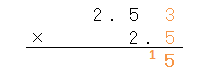
さっきの計算で繰り上がりの数「１」があるから、足し算すると「２６」だね。
つぎに、上の数の右端から三つ目の数「２」と、下の数の右端の数「５」をかけ算するんだよね。答えは「１０」だね。
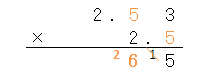
さっきの計算で繰り上がりの数「２」があるから、足し算すると「１２」だね。

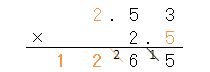
つぎは、下の数の、右から二つ目の数「２」で、さっきと同じように計算するんだったよね。
まず、上の数の右端の数「３」と、下の数「２」をかけ算するんだよね。答えは「６」だね。
答えを書くとき、一番小さな数が「２」の位置になるように書くんだったよね。

つぎに、上の数の右端から二つ目の数「５」と、下の数「２」をかけ算するんだよね。答えは「１０」だね。
つぎに、上の数の右端から三つ目の数「２」と、下の数「２」をかけ算するんだよね。答えは「４」だね。
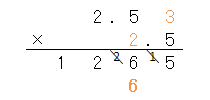
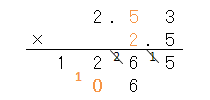
さっきの計算で繰り上がりの数「１」があるから、足し算すると「５」だね。

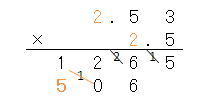
最後に、計算した数を足し算するんだったよね。
足し算する位を間違えないようにしよう。

足し算すると、６３２５、だね。
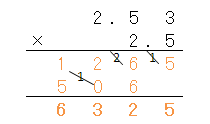
最後に、小数点を考えよう。
小数点はどこにつければいいのかな？

小数点は、かけ算した数の右端からの位置と同じ位置に、小数点をつけるんだったね。
「２．５３」の小数点は右端から２つ目、「２．５」の小数点は右端から１つ目だね。
この二つの場所を足し算すると、

だから、足し算した数の「６３２５」の右端から３つ目に小数点をつけるんだ。
だからひっ算は、
になるから、答えは、
だね。

「小数」のわり算

工事中。

「小数」のわり算のひっ算

工事中。