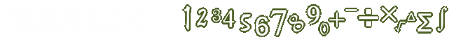ここでは、かけ算を使って文章問題を解こう。

全体の数を考えよう

さっそく、次の問題を考えよう。

さて、問題を図に描いてみよう。
まず、３人いたんだね。図を描くとこんな感じかな。

• 
• 
• 

つぎに、ひとり５個づつリンゴをとったんだね。図を描くとこんな感じかな。

• 
• 
• 

３人がとったリンゴの数はどうやって計算できるかな？
リンゴを一つづつ数えてもいいけど、かけ算を使った式（カッコイイ式）を考えよう。

全部のリンゴの個数は、「ひとりがとったリンゴの数（５個）」に「人数（３人）」をかければいいよね。
「ひとりがとったリンゴの数」は「５」個で、人数は「３」人だから、式は、

だね。
これを計算すると、
だから、答えは、
だ。

全体の数を考えよう２

次の問題を考えよう。

さっきのリンゴの問題と似ているね。
それでは、図を描こう。
レモンの全部の数はわからないけど、レモンは、１個残っているんだね。
また、３人いて、ひとり当たりレモンを５個持っているんだね。
図を描くとこんな感じかな。

• 
• 
• 

全部のレモンの数はどうやって計算できるか考えてみよう。

レモンには、「あまっているレモン」と「３人が持っているレモン」があるね。
だから、「全部のレモンの数」は「あまっているレモンの数」と、「３人が持っているレモンの数」を足すといいよね。
式で書くと、

だね。

まず、「あまっているレモンの数」は「１」個だね。

次に、「３人が持っているレモンの数」は、「ひとりが持っているレモンの数（５個）」に「人数（３人）」をかければいいよね。
式で書くと、

だね。

だから、「全部のレモンの数」を計算する式は、

になるね。

さあ、式を計算しよう。

だね。だから、答えは、
だ。

距離・長さを考えよう

次の問題を考えよう。

この問題は距離を計算しないといけないけど、どのように木を植えたかが分からないと、式も考えられないよね。
だから、はじめに図を描いて、木の植え方を理解してから、計算しよう。

それでは、図を描こう。
木が６本、まっすぐに植えているんだよね。
そして、木と木の間の距離は、４ｍ（メートル）だよね。
図を描くとこんな感じかな。


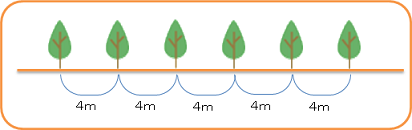
どうかな？　同じになったかな？

図がかけたから、今度は、どこの距離を答えればいいのか、図に書き込もう。
図を描くとこんな感じかな。


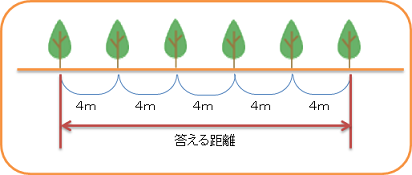
どうかな？　同じになったかな？

さて、図を見て、「答える距離」を計算する式を考えよう。

だね。
これを計算すると、
だね。だから、答えは、
だ。

ここで、次の問題を考えよう。

さっきの問題と同じだけど、よく見ると、木の本数が２１本になっているね。
図を描きたいけど、木を２１本も描くのは大変だし、数え間違えるかもしれないね。
そこで、さっきの問題の、木が６本の場合の図を使って、「木の本数」と「距離」との関係を考えて、計算してみよう。

木が６本のときの図は、

だったね。

さあ、木の本数と距離の関係を考えよう。

木が１本のときは、もう１本の木がないから、今は考えないでおこう。

何か、関係は無いかな？
・・・！
木が１本増えるごとに、距離が４ｍ増えているね。
じゃあ、距離は４のかけ算を使って書けるんじゃないかな？

よく見ると、「距離」は「４」×「木の本数－１」になっているね。
「木の本数」と「距離」との関係を発見したよ！

式は、

だね。

さあ、問題に戻ろう。問題は、

だから、見つけた法則に当てはめると、
だね。「木の本数－１」を初めに計算するからカッコを書いたよ。
これを計算すると、
だね。だから、答えは、
だ。