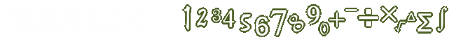ここでは、「距離(きょり)」と「速さ」の計算を説明するよ。
「距離」を計算しよう
「距離」は「ある2点間を測定した長さ」だったね。
ここでは、「距離」を計算してみよう。
「距離(きょり)」ってなに?って思った人は「距離ってなに?」のページで一緒に考えよう。
次の問題を考えてみよう。
車の速さは、時速40kmでした。
花子さんの自宅から富士山までの道のりは何kmですか?
「自宅から富士山までの道のり」は、「車で走った距離」だよね。
「車で走った距離」を計算するには、どうすればいいんだろう?
問題を考える前に、「時速2km」の場合を考えてみようだよね。
「時速2km」は「1時間に2km進む」ってことだよね。
では、「2時間」では、どのくらい進むのだろう?
「1時間」で「2km」進むから、「2時間」では「4km進む」よね。
では、「3時間」では、どのくらい進むのだろう?
「1時間」で「2km」進むから、「3時間」では「6km進む」よね。
つまり、「進んだ距離」は、
さぁ、問題を考えよう。
上で考えたように、「車で走った時間」は、
問題文から、
「車で走った時間」は、2時間
だから、
=40×2
=80
「車で進んだ距離」は80kmだから、答えは、
「速さ」を計算しよう
「速さ」は「一定時間あたりに進む距離」だったね。
ここでは、「速さ」を計算してみよう。
「速さ」ってなに?って思った人は「速さってなに?」のページで一緒に考えよう。
次の問題を考えてみよう。
ベンチから風車までの道のりは200メートルです。
花子さんは、秒速何メートルで走ったのでしょうか?
「秒速」は、「1秒あたりに進んだ距離」だよね。だから、1秒間に進んだ距離を計算すればいいんだ。
では、「1秒あたりに進んだ距離」を計算するには、どうすればいいんだろう?
問題文を読むと、花子さんは、「40秒」で「200メートル」進んだよね。
では、半分の時間の「20秒」では、どのくらい進むんだろう?
そう、「20秒」では、半分の距離の「100メートル」進むよね。
では、さらにその半分の時間の「10秒」では、どのくらい進むんだろう?
そう、「10秒」では、さらに半分の距離の「50メートル」進むよね。
では、「10秒」で「50メートル」進んだから、「1秒」では、どのくらい進むんだろう?
そう、「50メートル」を「10秒」で割ると、1秒間で進む距離(秒速)になるよね。
つまり、「1秒あたりに進んだ距離」は、
問題文から、
「かかった時間」は、40秒
=200÷40
=5
「1秒あたりに進んだ距離」は「5メートル」だから、答えは、
では、つぎの問題。
では、花子さんは、時速何メートルで走りますか?
問題は、花子さんが、時速何メートルで走っているかを答えればいいよね。
「時速」ってなんだったかな?
そうだね。「1時間あたりに進む距離」だったよね。
じゃあ、花子さんが1時間で進む距離を計算しよう。
秒速5メートルってことは、1秒間に5メートル進むよね。
1時間は3,600秒だから、どれくらい進むのかな?
まず、1秒だと、5メートル。
2秒だと、10メートル進むよね。
3秒だと、さらに5メートル進むから、15メートル進むよね。
4秒だと、さらに5メートル進むから、20メートル進むよね。
このまま3,600秒まで計算すると大変だね。
もっとカッコいいやり方を探そう。
何かきまりはないかな?
そうだね。
1秒だと5メートル
2秒だと10メートル。これは5×2だよね。
3秒だと15メートル。これは5×3だよね。
4秒だと20メートル。これは5×4だよね。
つまり、「走った距離=5×かかった時間(秒)」だね。
これを使って、3,600秒で走った距離を計算すると、
=5×3600
=18000
これは1時間あたりに進む距離(メートル)だから、答えは、
ちなみにだけど、
だから、
2キロメートル=2,000メートルだよね。
3キロメートル=3,000メートルだよね。
4キロメートル=4,000メートルだよね。
このまま、18,000メートルまで考えるのは、大変だね。
何か決まりはないかな?
そうだね。
キロメートルの数に、1000をかけると、メートルになっているよね。
たとえば、
2キロメートルだと、2×1000=2,000メートルだよね。
逆に、メートルの数を、1000で割ると、キロメートルになっているよね。
たとえば、
2000メートルだと、2000÷1000=2キロメートルだよね。
これを使って、
では、つぎの問題。
秒速30メートルの台風の風の速さは、
どちらの方が速いでしょう?
はじめに気が付くのは「40キロメートル」と「30メートル」とでは単位が違うよね。
一方は「キロメートル」、もう一方は「メートル」だよね。
速さを比べるには、まず単位を合わせよう。
1キロメートル=1,000メートルだから、 40キロメートルは、
=40,000メートル
つまり、時速40キロメートル=時速40,000メートル。
2.台風の風の速さ、秒速30メートル
ちょっとまって! もう一つ単位が違うよ。
「時速」と「秒速」だね。
「秒速」は「1秒間あたりに進む距離」
さっきの速さをもう一度みなおそう。
「1時間」は「3,600秒」だから、「時速」は「3,600秒あたりに進む距離」だね。
だから、下のどちらかを計算して、単位を合わせる必要があるよ。
2.車の速さ「時速40,000メートル」を、「秒速」に計算しなおす。
ここでは、「1.台風の風の速さ、秒速30メートル、を、時速に計算しなおす」をするよ。
「秒速」を「時速」にするには、どうすればいいんだろう?
時速=1時間に進む距離=3,600秒間に進む距離
では、どうやって計算すればいいんだろう?
たとえば「秒速1m」では「1秒間に1m進む」から、「1時間=3,600秒」では「3,600m進む」よね。
つまり、
これを使って、秒速30メートルを時速を計算すると、
=108,000
これで、「車の速さ」と「台風の風の速さ」が「1時間当たり何メートル進むか」を計算できたので、速さを比べてみよう。
=時速40,000メートル
2.台風の風の速さ=秒速30メートル
=時速108,000メートル
車の速さは時速40キロメートル、台風の風の速さは秒速30メートル、だったから、車の方が速く思えるけど、計算して単位を合わせると、台風の風の速さの方がとても速いね。
比べるときは単位を同じにするように気を付けよう。
では、次の問題を考えてみよう。
今度は、「単位」に注意しよう。
花子さんの歩く速さは、分速50mです。
花子さんの自宅から風車までの道のりは何kmですか?
「自宅から風車までの道のり」は、「歩いた距離」だよね。
「歩いた距離」を計算するには、
「歩いた時間」は、2時間
だから、
「歩く速さ」は、「分速50m」だから、「1分間あたりに50m進む」ということだよね。
一方、「歩いた時間」は、「2時間」だよね。
「歩く速さ」は「1分間あたり」なのに、「歩いた時間」は「時間」が単位だから、単位が違うよ。
計算するには、下のどちらかを計算して、単位を合わせる必要があるよ。
2.歩いた時間の「2時間」を、「分」に計算しなおす。
ここでは、「2.歩いた時間「2時間」を、「分」に計算しなおす」をするよ。
「1時間」は「60分」だから、
=2×60分
=120分
=分速50m×120分
=6,000m
問題の質問は「花子さんの自宅から風車までの道のりは何kmですか?」だから、
「歩いた時間」の単位を「メートル」から「キロメートル」に変えるには、1,000m=1kmだから、
=6km
だから、答えは、
速さと時間と距離を考えるときは、単位を同じにするように気を付けよう。
たとえば、下のように単位を合わせよう。
時間:○○秒
距離:○○m
時間:○○秒
距離:○○m
「時間」を計算しよう
ここでは、「ある速さ」で「ある距離」を進むのに要する「時間」を考えよう。
次の問題を考えよう。
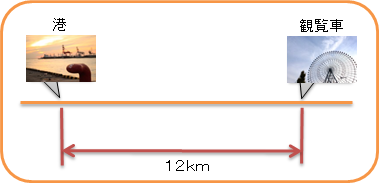
自転車の速さは時速4kmで、港から観覧車は12km離れていました。
太郎さんは、港から観覧車まで、何時間かかりましたか?
さて、「港から観覧車までのかかった時間」をどうやって計算しよう。
図を描いて考えてみよう。
太郎さんは、自転車に乗って時速4kmで港から出発したんだよね。
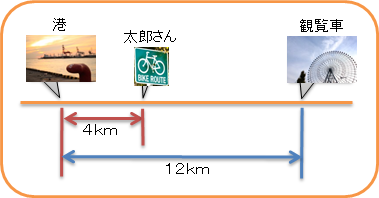
では、1時間後には、太郎さんはどこにいるのかな?
そう、1時間後には、港から4kmの場所だよね。
図を描くとこんな感じかな。
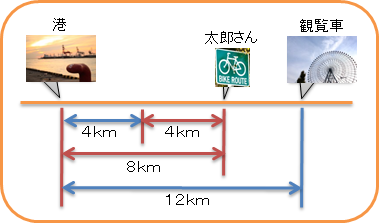
では、2時間後には、太郎さんはどこにいるのかな?
そう、さっきの場所から4km進んだ場所だよね。これは港から8kmの場所だよね。
図を描くとこんな感じかな。
では、3時間後には、太郎さんはどこにいるのかな?
そう、さっきの場所からさらに4km進んだ場所だよね。これは港から12kmの場所だよね。
図を描くとこんな感じかな。
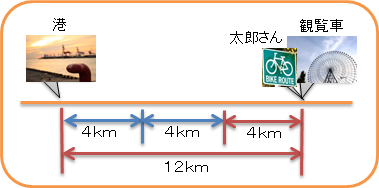
あっ、港から12kmの場所は、観覧車のある場所だよね。
太郎さんは、3時間で観覧車についたね。
だから、
答えは合っているけど、計算して答えを出すにはどうすればいいんだろう?
もう一度、図を見よう。

全体の距離「12km」には、自転車が1時間に進む距離「4km」が、「3つ」含まれていることが分かるね。
つまり「全体の距離」を、「速さ」で割ると、「かかった時間」が計算できるんだ。
式で書くと、
「1時間に進む距離(時速)」は、4km
=12÷4
=3
だから、答えは、
距離・速さの説明はここでおわりだよ。