ここでは、「速さ」を説明するよ。
「速さ」ってなに?
「速さ」について考えよう。
「速さ」とは、「一定の時間にどのくらいの距離を進めるか」を表したものなんだ。
「一定の時間」っていうのは、たとえば「1秒間」や「1時間」なんだ。
「速さ」を言うときだけど、
2)新幹線の速さは、250km毎時だ。
3)台風の風の速さは、30m毎秒です。
(風の速さは「秒速」で考えることが一般的だから、
「風速30m」と書くこともあるよ。)
2)新幹線の速さは、時速250kmだ。
3)台風の風の速さは、秒速30mです。
「1時間あたりに80km進む」ということ。
「1時間あたりに250km進む」ということ。
「1秒間あたりに30m進む」ということ。
どちらも同じ意味だから、どちらを使ってもいいよ。
「km毎時」や「m毎秒」、「時速~km」や「秒速~メートル」は、一定の基準を表していて、「単位」と呼ぶんだ。
速さの単位には距離の単位(kmやm)と時間の単位(時や分、秒)を組み合わせた、「km毎時」や「m毎分」「m毎秒」などを使うから覚えておこう。
速さとは「一定の時間にどのくらいの距離を進めるか」を表した数だったよね。
では次の問題を考えよう。
自転車は1時間でどれだけの距離を進みますか?
だから、答えは、
では次の問題を考えよう。
車は1時間でどれだけの距離を進みましたか?
だから、答えは、
では次の問題を考えよう。
カタツムリは1分間でどれだけの距離を進みますか?
だから、答えは、
「分速」だから「一定の時間」が「1分間」になることに注意しよう。
それと、距離が「cm」になっていることにも注意しよう。
では次の問題を考えよう。
では、自転車は2時間でどのくらいの距離を進むでしょうか。
では2時間ではどのくらいの距離を進むかな?
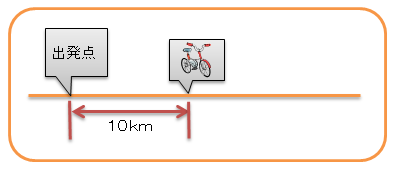
はじめに出発してから、1時間たったときを考えよう。
自転車は10km進んでいるよね。
図で書くとこんな感じかな。
つぎに、上の図からさらに1時間たったときを考えよう。出発してからは2時間たったときになるね。
自転車は、10km毎時で進むから、上の図から、さらに10km進んでいるよね。
図で書くとこんな感じかな。
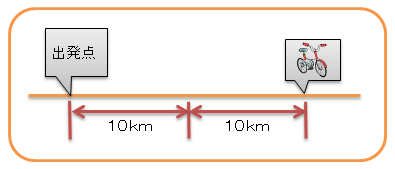
つまり、2時間では、10km+10km=20km進んでいるね。
だから、答えは、
さっきは図を描いて考えたけど、式で書いてみよう。
自転車の進む距離は、時間がたった分だけ増えるから、速さに時間をかけ算すればいいよね。
(速さを時間で割ると、時間がたった分だけ、進む距離が短くなっちゃうよ。そんなの変だよね。)
10km毎時×2時間=20km。
よって、自転車は2時間で、20km進む。
では次の問題を考えよう。
自転車は10km毎時の速さで進みます。
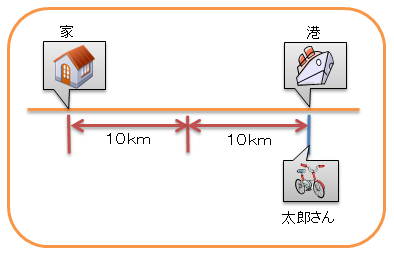
太郎さんの家から港までの道のりは何kmでしょうか。
家から港までの距離は、自転車が2時間に進む距離と、同じだよね。
なぜなら、家から港まで、自転車に乗って2時間で着いた、からね。
図を描くとこんな感じかな。
1時間後
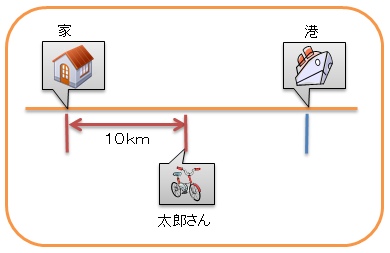
2時間後
だから、答えは、
図を使わずに書くと、
自転車の速さは10km毎時だから、2時間で進む距離は、
10km毎時×2時間=20km。
よって、家から港までの距離は、20km。
速さの単位を変えてみよう
速さの単位には、「km毎時」や「cm毎分」、「m毎秒」などがあるね。
たとえば、高速道路を走る車の速さと、台風の風の速さを比べたいときはどうすればいいんだろう?
車の速さは「1時間あたりに何km進むか」で表すよね。
「車で高速道路を100km毎時で走行する」っていうよね。
一方風は、台風のときとか、「風速30m毎秒の暴風」っていうよね。
この2つはどっちの方が速いんだろう?
上の問題は後から考えよう。
まずは次の問題を考えよう。
なぜなら、「60km毎時」は「1時間に進む距離」で、「1km毎分」は「1分間に進む距離」だよね。
1時間は60分間だから、「60km毎時」は「60分間に進む距離」ともいえるね。
「60分間に進む距離」と「1分間に進む距離」とそのまま比べても、どちらが速いかはわからないよね。
だから、速さを比べるときは、単位をそろえる必要があるんだ。
単位はどんな単位にそろえてもいいよ。
大事なのは単位をそろえることなんだ。
今回は「km毎時」の単位にそろえてみよう。
「60km毎時」は単位が「km毎時」だからそのままでいいよね。
「1km毎分」は単位が「km毎分」だから単位を変えないといけないよ。
では、単位を変えてみよう。
「1km毎分」を「km毎時」に変えてみよう。
「毎分」を「毎時」に変えるには、1時間に進む距離を考えればいいんだ。
1時間=60分、だよね。
だから、「1km毎分」の速さで60分間で進む距離は、
だから、「1km毎分」の速さは「60分間に60km進む」速さと同じだよね。
言いかえると、「1km毎分」の速さは「1時間に60km進む」速さと同じだよね。
さらに言いかえると、「1km毎分」の速さは「60km毎時」の速さと同じだよね。
だから、問題の答えは、
答え)
「1km毎分」=「60km毎時」だから、同じ速さ。
次の問題を考えよう。
でも単位がちょっと違うよ。
「m」と「km」だね。
このままだと比べられないね。
速さを比べるときは、単位をそろえる必要があるんだったね。
単位を同じにしよう。
今回は単位を「m毎分」にそろえてみよう。
「3000m毎分」の単位は「m毎分」だからそのままでいいよね。
「3km毎分」は単位が「km毎分」だから単位を変えないといけないよ。
では、単位を変えてみよう。
「3km毎分」を「m毎分」に変えてみよう。
「k」は1000倍を表す接頭辞だったから、「k」を使わないときは、数を1000倍にすればいいよね。
=3000m毎分
だから、問題の答えは、
答え)
3km毎分=3000m毎分、だから、同じ速さ。
それでは次に、最初の疑問を考えよう。
単位が違うからこのまま数を比べられないよね。
速さを比べるときは、単位をそろえる必要があるんだよね。
今回は「km毎時」の単位にそろえてみよう。
「100km毎時」は単位が「km毎時」だからそのままでいいよね。
「30m毎秒」は単位が「m毎秒」だから単位を変えないといけないよ。
では、単位を変えてみよう。
はじめに「m毎秒」を「m毎時」に変えて、つぎに「m毎時」を「km毎時」に変えよう。
「毎秒」を「毎時」に変えるには、1時間に進む距離を考えればいいんだったよね。
1時間=3600秒間だから、「30m毎秒」の速さで3600秒間で進む距離は、
だから、「30m毎秒」の速さは「3600秒間に108000m」速さと同じだよね。
言いかえると、「30m毎秒」の速さは「108000m毎時」の速さと同じだよね。
「108000m毎時」の速さと同じだよね。
次に、「m毎時」を「km毎時」に変えるよう。
「k」は1000倍を表す接頭辞だったから、「k」を使うときは、数を1000で割ればいいよね。
=108km毎時
だから、問題の答えは、
答え)
「30m毎秒」=「108km毎時」だから、風の方が速い。