ここでは、かけ算・カッコを学ぼう。

かけ算はたし算をカッコ良くしたもの？！

「かけ算」ってなんだろう。
かけ算を考える前に、次の問題を計算してみよう。

この式を計算すると・・・そう、

だから、答えは６だね。

次はどうかな？

この式を計算すると・・・・そう、 だから、答えは１２だね。

次はどうかな？

この式を計算すると・・・・・・・・そう、 だから、答えは２４だね。

ここで、どのように計算したか考えてみよう。
下のように、３を前から順に足して計算したかな？

この方法だと７回計算すれば、答えが出るね。
他の方法で計算した人もいるかな？

実はかけ算を使うととても便利なんだ。

さっきの、

を、かけ算で書くと、
になるんだ。
式がとても短くなったね。
「×」は「かける」と読むんだ。上の式は「３ かける ８」だね。

では、「×」の意味を考えてみよう。

「×」の記号は、「×の前の数」が「×の後の数」だけある、という意味なんだ。
上の式では、「３」が「８」個ある、という意味なんだ。
だから、３を８個足した式と、「３×８」は同じ意味だし、同じ答えになるんだね。

ところで、「３×８」はどうやって計算するんだろう？
「３」を８回たして計算してもいいけど、かけ算はもっと便利な方法があるんだ。
たし算とちがって、かけ算は「九九」（「くく」って読むよ）を使って計算するんだ。
かけ算を使うと式がとても短くになってカッコイイし、計算も早くできるからるから、「九九」は必ずおぼえよう。

「九九」はこちら

かけ算を使ってみよう

さて、かけ算ってどんな時に使うんだろう？

下の問題を考えてみよう。

さぁて、どうやって計算しようか？？
はじめに、考えやすいように、図(絵)をかいてみよう

リンゴが３個入った箱　　が４箱なので、
図をかくとこんな感じかな。

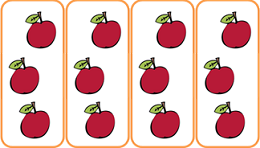
「３」が「４」つあるから、たし算で書くと、

だね。

このまま計算してもいいんだけど、カッコいいかけ算を使って計算しよう！

「３」が「４」つあるから、これをかけ算で書くと、

だね。

この式を「九九」を使って」計算すると・・・、

だね。
だから、リンゴは１２個だ。

それでは次の問題を考えよう。

はじめに図をかこう。
図をかくとこんな感じかな。

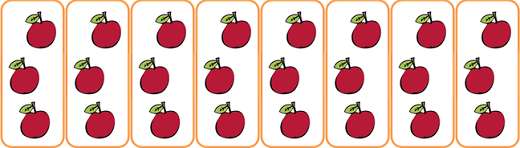
カッコいいかけ算で式を考えてみよう。
「３」が「８」つあるから、

だね。

この式を「九九」を使って計算すると・・・、

だから、リンゴは２４個だ。

もっと、かけ算を使ってみよう

いままではリンゴが同じ数入っている箱を考えたけど、次の式はどうなるかな？

さっきと同じように考えてみよう。

まず、図を描いてみよう。。。描けたかな？
「タロウくんと花子さんのリンゴを合わせた数」を計算する式は、

を計算すればいいんだ。

そこで、「タロウくんのリンゴの数」と「花子さんのリンゴの数」を考えるよ。
「タロウくんのリンゴの数」は、「リンゴが２個入った箱」が「３箱」だから、「２」が「３」つだ。式にすると、

だね。

つぎに、「花子さんのリンゴの数」は「リンゴが３個入った箱」が「２箱」だから、「３」が「２」つだ。式にすると、

だね。

では、これをもとに、「タロウくんと花子さんのリンゴを合わせた数」をもう一度考えよう。
「タロウくんと花子さんのリンゴを合わせた数」は、

だったね。

「タロウくんのリンゴの数」は「２×３」、「花子さんのリンゴの数」は「３×２」だから、

になるね。

これを計算すると、、、あれ？　かけ算とたし算の両方があるよ。
どこから計算すればよいのかな？

「２×３＋３×２」はどこから計算するのかな？
最初に計算するのは、次の３つのうちのどれかな？

正解は［１］と［３］のどちらでもいいんだ。
気を付けるのは、かけ算はたし算より先に計算するってことなんだ。
たし算より先にかけ算を計算する決まりについては、次の「たし算より先にかけ算を計算するのはなぜ？」で考えよう。

それでは、「タロウくんと花子さんのリンゴを合わせた数」

を計算してみよう。

「２×３＝６」だから、

だね。

つぎに「３×２」を計算しよう。
「３×２＝６」だから、

だね。

この式を計算すると・・・、

だね。だから、答えは、
だね。

かけ算はたし算より先に計算しよう

下の３つの式は、全部３が４つあるといくつになるか、を計算する式だ。
答えも、もちろん同じになるんだ。

［１］は、３を４つ分足しているね。
［２］は、３が４つあることをかけ算で書いてるね。
［３］は、３が２つ（３×２）と、３が２つ（３×２）を足しているから、全部で３が４個あることを書いてるね。

それでは、計算してみよう。

［１］の式を計算すると、

で、答えは １２ だね。

［２］の式を計算すると・・・、

で、答えは １２ だね。［１］と同じになったね。

さあ、次は［３］の式だ。

たし算とかけ算があるときは、かけ計から計算するんだったね。
それでは、計算しよう。
で、答えは １２ だね。
［１］や［２］と同じになったね。

［１］［２］［３］の式は、３が４つでいくつになるか、を計算する式だから、答えは同じになるんだ。

では、かけ算をたし算より先に計算しなかったらどうなるか、さっきの［３］の式で試してみよう。

はじめに、たし算を計算すると、

もう間違えていることに、気が付いたかな？
「３×５×２」の式はかけ算だから、「３」が「５」つあって、それが「２」つあることを表しているよ。
リンゴで考えてみると、リンゴ「３」個が入っている箱が「５」箱あって、それがさらに「２」つある、ってことだから、図を描くと下のようになるよ。

「３」が「４」つの式だったのに、全然違うことを計算してしまっているよ。。。

たし算とかけ算があるときは、計算する順番が大切なんだ。必ずかけ算から計算しようね。

でも、かけ算より先に、たし算から計算したいときもあるよね。
次の「かけ算より先にたし算を計算するには？（カッコを使おう）」で考えよう。

かけ算より先にたし算を計算するには？（カッコを使おう）

いきなりだけど、次の問題を考えてみよう。

図を描くとこんな感じかな。

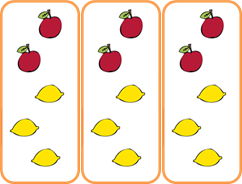
では、式を考えよう。
実は、式は次の二通りを考えられるよ。
　［１］　リンゴの数とレモンの数を別々に数えてから、合わせた個数を計算する。
　　　　　図を書くとこんな感じかな。
　　　　　
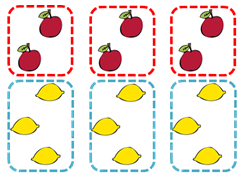
　　　　　計算の順番は、
　　　　　　１．　ひと箱のリンゴの数（赤枠）を考えて、３箱分の数を計算する。
　　　　　　２．　ひと箱のレモンの数（青枠）を考えて、３箱分の数を計算する。
　　　　　　３．　リンゴ３箱分とレモン３箱分の数を合わせる。
　　　　　といいよね。

　［２］　ひと箱に入っているリンゴとレモンを合わせた数が、何箱あるかを計算する
　　　　　図を描くとこんな感じかな。
　　　　　
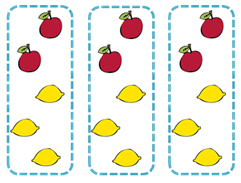
　　　　　計算は、
　　　　　　・ひと箱のリンゴとレモンの合わせた数（青枠）を考えて、３箱分の個数を計算する。
　　　　　といいよね。

それぞれの考え方で計算してみよう。

［１］の考え方で計算しよう

それでは、
　［１］　リンゴの数とレモンの数を別々に数えてから、合わせた個数を計算する
の考えた方で、リンゴとレモンを合わせた個数を考えよう。

図を書くとこんな感じだよね。

初めに、リンゴの数とレモンの数を別々に数えると、

だ。

だから、リンゴとレモンは合わせた個数を計算する式は、

だ。

では、この式を計算していこう。
「リンゴが２個入った箱」が「３箱」を式にすると、

だ。

つぎに、「レモンが３個入った箱」が「３箱」を式にすると、

だね。

だから、リンゴとレモンは合わせた式は、

だね。

この式を計算すると、

だね。だから、答えは、 だね。

［２］の考え方で計算しよう

それでは、
　［２］　ひと箱に入っているリンゴとレモンを合わせた数が、何箱あるかを計算する
の考えた方で、リンゴとレモンを合わせた個数を考えよう。

図を書くとこんな感じだよね。

初めに、「ひと箱に入っているリンゴとレモンを合わせた数」を数えると、

だね。

この箱が ３箱あるから、式は、

だ。、、、と書きたくなるけれど、これだと計算が合わないんだ。
なぜかというと、たし算とかけ算はかけ算を先に計算する、という決まりがあるから、
これを計算すると、
となって、答えが合わなくなってしまうんだ。

ではどうすればいいのかな？ ここで新しい記号「カッコ（）」を使うんだ。

式にカッコがあるときには、「カッコの中から先に計算する」という決まりがあるんだ。
では、さっそくカッコを使ってみよう。

さっきの式にカッコを書き加えて、

と書こう。これで、箱の中のリンゴとレモンを合わせた数（２＋３）を先に計算できるよ。

この式を計算すると、

だね。だから、答えは、 だね。

これで、［１］の式とも答えが一緒になったね。
次はカッコを使った計算をもう少し考えてみよう。

カッコを使った計算

式にカッコがあるときは、カッコの中を先に計算するという決まりがあるんだったね。
カッコがあるときと、ないときで計算の順番が変わるよ。
ためしに、次の２つの式を計算してみよう。

とても似た式だけど、［２］はカッコの中にたし算があるよ。

>

はじめに ［１］ の式から計算してみよう。たし算とかけ算だから、かけ算を先に計算するよ。

で、答えは ７ だね。

次は ［２］ の式を計算してみよう。
たし算とかけ算だから、かけ算を先に計算するのかな？
気を付けて！　カッコがあるよ！　カッコの中から先に計算しよう！

で、答えは ９ だね。

カッコがあるときは気をつけて計算しよう。

そうそう、さっきカッコの中を計算した後、カッコを途中から書かなかったね。
カッコの中が数字だけになった時は、カッコは書かないんだ。

［２］ の式をもう一度計算してみよう。カッコの中を計算すると、

と書きたくなるけれど、カッコの中が数字だけになっているからカッコは書かないんだ。

だから、

と書くんだ。

さぁ、これまで学んだ計算の順序をまとめると、次の通りだよ。

ではここで問題。次の式を計算してみよう

たし算、かけ算、カッコが混ざっているから計算の順番に注意しよう。 では、計算してみよう！

カッコがあるから、カッコの中から計算するんだったね。カッコの中の式に色を付けると下記になるね。

あれ？　カッコの中にカッコがあるよ？！

落ち着いて考えよう。やっぱりカッコを先に計算するんだ。
だから、一番最初に計算する個所は「１＋１」になるよ。

これを計算すると、

次に計算する場所は、カッコの中の式の、

だ。

かけ算はたし算より先に計算するから、

だ。

最後に、

を計算すると、
で、答えは １２ だね。

計算の順番は、落ち着いて考えれば難しくないね。

計算問題を解こう

それでは、これまで学んだことを使って、問題を解いてみよう。

ここからは計算の順番に注意しよう。

ここからは、カッコが出てくるよ。計算の順番に注意しよう。

次は文章を読んで考えよう。

ここからは、学んだことを思い出してチャレンジしよう。

最後の問題だよ。

では、答え合わせをしよう。

問題１と問題２は九九を使って計算しよう。

問題３～５は、たし算より先にかけ算を計算しよう。

カッコがあるときは、カッコの中を先に計算するんだったね。

文章の問題は図を描いて考えよう。

これを図に書くと、下のようになるね。

式は、たし算だけで書いてもいいし、かけ算を使って書いてもいいね。

これを計算すると、答えはどちらも１２になるね。
だから答えは、

だ。

問題９～１１は次の決まりを思い出して計算しよう。

最後の問題１２は、図を考えながら解いてみよう。

文章の問題は図を描いて考えよう。
これを図に書くと、下のようになるね。

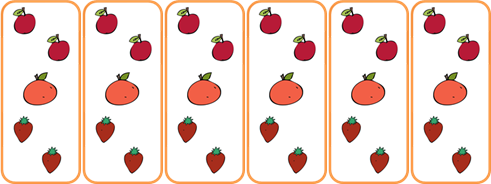
式は下の二つが考えられるね。他の式を考えた人もいるかな？

この式を計算すると、どちらも３０になるね。
だから答えは、

だ。

かけ算の説明はここでおわりだよ。次はわり算にチャレンジしよう。