ここでは、わり算を説明するよ。

わり算は「みんな同じ」が好き？！

「わり算」ってなんだろう。
その前に、次の問題を考えてみよう。
さて、どうやって計算しよう・・・
そうだね、図を描いて数えよう。
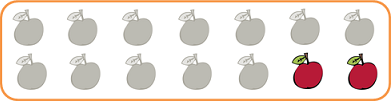
リンゴが６個あるね。図をかくとこんな感じかな。



それとリンゴを分け合う３人も呼ぼう。
図を描くとこんな感じかな。

• 
• 
• 

はじめに、一人にリンゴを一個ずつ配ってみよう。

• 
• 
• 

まだ、リンゴは残っているね。リンゴをもう一個ずつ配ってみよう。

• 
• 
• 

もうリンゴは残っていないよ。
リンゴ６個を、３人で等しく分けると、一人当たりリンゴが２個になるね。
だから、問題の答えは、
だね。

リンゴを分けることと、わり算が関係があるかって？
実は、はじめにあったリンゴを、みんなで等しく分けて、一人あたりの数を計算すること、がわり算をすることなんだ。

わり算の書き方は、

なんだ。
「わり算」の記号は「÷」だ。「÷」は「わる」と読むんだ。
さっきの、リンゴ６コを３人で分ける計算をわり算で書くと、
「全体の数」はリンゴ「６」コ、「わける数」は「３」人だから、
と書くんだ。

わり算の書き方は、

だったよね。
では、わり算の答えはなんだろう？
実は、「１あたりの数」なんだ。
「１あたりの数」は、リンゴ６コを、３人で分けたときの、「一人あたりのリンゴの数」のことなんだ。
リンゴ６コを、３人で分けると、「一人あたりのリンゴの数」は「２」コだから、
になるんだ。

「６÷３」の答え「２」は絵を描いて考えた答えだけど、もっとカンタンに計算できないか、考えてみよう。
実は、「６÷３」の答えは、

の式の、？に当てはまる数なんだ。
九九を思い出そう・・・！

「３×２＝６（さん　に　が　ろく）」だったね。
だから、「６÷３」の答えは、
なんだ。

「６÷３」の答えが、

の式の、？になるのはなんでだろう？
考えてみよう。

を、言葉で書きかえると、
になるね。
リンゴの問題で書きかえると、
「１あたりの数」は、「一人あたりのリンゴの数」、「分ける数」は、「リンゴを分けた人数」だから、
になるね。

あれ？　どこかで見た式だね。
そう、かけ算の式と同じなんだね。
かけ算で下の問題を考えたとき、

全部のリンゴの数を計算するには、かけ算を使って、
と書けるね。

わり算は、かけ算とは逆に、「全体の数」から「一人あたりのリンゴの数」や「リンゴを持っている人数」を計算することができるんだ。

わり算を使ってみよう

次の問題を考えてみよう。

さて、「一人あたりが持っているリンゴの数」をどうやって計算しよう・・・
まず、わかっていることをまとめよう。
だね。

「１あたりの数」が分からないから、計算しないとね。
「全体の数」と「分けた人数」が分かっているから、「１あたりの数」はわり算を使って計算できるね。
「１あたりの数」を計算する式は、わり算を使って、

だね。
これに、分かっている数字をあてはめると、
だね。

「１２÷３」の答えは、「３×？＝１２」になる「？」の数字だ。
九九を使って考えると、「３×４＝１２（さん　し　じゅうに）」だから、「？」は「４」だね。
だから、さっきの式は、

だね。だから、答えは、
だね。

次の問題を考えてみよう。

さて、「リンゴをわけた人数」をどうやって計算しよう・・・
まず、わかっていることをまとめよう。
だね。

「リンゴをわけた人数」が分からないから、計算しないとね。
「全体の数」と「１あたりの数」が分かっているから、「分けた人数」は、わり算を使って計算できるね。
「分けた人数」を計算する式は、わり算を使って、

だね。
これに、分かっている数字をあてはめると、
だね。

「１６÷４」の答えは、「４×？＝１６」になる「？」の数字だ。
九九を使って考えると、「４×４＝１６（し　し　じゅうろく）」だから、「？」は「４」だね。
だから、さっきの式は、

だね。だから、答えは、
だね。

もっと、わり算を使ってみよう

これまではリンゴがちょうど分け合えたけど、リンゴが余（あま）ったときはどうなるんだろう？
次の問題を考えよう。

さて、「一人あたりが持っているリンゴの数」と「余ったリンゴの数」をどうやって計算しよう・・・
まず、わかっていることをまとめよう。
だね。

では、図を描いて考えてみよう。
リンゴが１４個あって、３人で分け合うんだよね。
リンゴを配る前の図を描くとこんな感じかな。

• 
• 
• 

では、みんなにリンゴをどんどん配（くば）ろう。
配るときには、みんなが持っているリンゴの数が等しくなるように気を付けよう。

リンゴを配った後の図を描くとこんな感じかな。

• 
• 
• 

まだ、リンゴが２コ残っているね。
でも、３人に配るにはリンゴが足りないから、もう配れないね。

さて、「一人あたりが持っているリンゴの数」と「余ったリンゴの数」はいくつかな？
図からわかるね。答えは、

だね。

さっきの問題は、図に描いて考えたけど、リンゴが多くなると、図に描けなくなるね。
それに、図を描くのは時間がかかるね。
もっとカンタンに、速く答えを出す方法はないか、考えてみよう。

下の問題のように、リンゴがちょうど配れたときは、わり算で計算したよね。

式は
だったね。

同じように、計算できると、イイよね。
実は、その方法があるんだ。

さっきの問題は、

だったね。
これを同じように、式で書くと、
だね。
これを計算しても、「３×？＝１４」に当てはまる「？」はないよね。
そんなときは、１４をこえない、一番大きな数を考えるんだ。
１４をこえない一番大きな数は「３×４＝１２」だね。
だから、まず「４」を書くんだ。
そして、ここからが大事なんだけど、「１４」からさっきの「１２」をひき算した答え「２」を、「４」の後に、「・・・」と書いた後に書くんだ。
さぁ、式の続きを書くと、
になるんだ。これで式が完成だ。
「４・・・２」は、「４　あまり　２」と読むんだ。
これは、「１４」を「３」で割ると、１あたりの数が「４」で、「２」余る、という意味なんだ。
つまり、
という意味なんだ。
さっき考えた図と同じになっているね。

わり算で、割り切れないときでも、計算できる方法を覚えていると便利だよね。
忘れないでおこう。

次の問題を考えてみよう。

さて、「リンゴをわけた人数」をどうやって計算しよう・・・
まず、わかっていることをまとめよう。
だね。
他に、考えられる数はないかな？
・・・そうだね！　配ったリンゴの数も計算できるよね。
配ったリンゴの数は、「全体の数」－「余ったリンゴの数」だね。
だから、
だね。

では、何人で分けたかを考えてみよう。
「配ったリンゴの数」が１８コで、一人あたり３コだから、

だね。だから、答えは、
だね。

わり算とかけ算はどっちを先に計算？

わり算とかけ算はどっちを先に計算するんだろう？
実は、わり算とかけ算は順番を入れ替えて計算しても良いんだ。
また、わり算は、かけ算と同じで、たし算とひき算より、先に計算するんだ。
なるべく、計算まちがいをしないように、工夫して、計算しよう。

次の式を計算してみよう

どうやって計算しよう？

はじめに、前から順番に計算してみよう。

だから、答えは、「１０」だね。

次に式の順番を入れ替えて計算してみよう。

かけ算とわり算は式を入れ替えることができるから、下の式のように入れ替えよう。
入れ替えるときには、数字の前に付いている記号（÷や×）も忘れずに一緒に移動しよう。

では、前から順番に計算してみよう。
だから、答えは、「１０」だね。

さっきは、式を下のように書き換えたけど、

書き換えずに、そのまま計算してもいいんだよ。

どっちが計算しやすかったかな？