分数のたし算
次の問題を考えてみよう。
一人あたりが食べたリンゴは何個ですか?
その後、リンゴを3個買ってきて、6人で分けて食べました。
一人あたりが食べたリンゴは、さっき食べたリンゴと合わせて何個になりますか?
さあ、考えよう。
問題文を読むと、リンゴを二回食べていることがわかるね。
はじめは、リンゴ2個を6人で分けて食べたね。
次に、リンゴ3個を6人で分けて食べたね。
質問は、一人あたり、リンゴを合わせて何個食べたか、だよね。
だから、一回目に食べた数と、二回目に食べた数を計算して、たし算しよう。
はじめに、一回目に食べたリンゴの個数を計算しよう。
リンゴ2個を6人で分けたから、一人あたりのリンゴの数は、
=
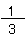
つぎに、二回目に食べたリンゴの個数を計算しよう。
リンゴ3個を6人で分けたから、一人あたりのリンゴの数は、
=

これで、一回目と二回目に食べたリンゴの数が分かったね。
一回目は、 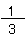 コ、二回目は、
コ、二回目は、  コだね。
コだね。
さぁ、計算しよう!
分数は、分子と、分母があるけど、どうやって計算するんだろう?
分子は分子でたし算して、分母は分母でたし算するのかな?
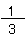 +
+  は
は 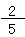 かな?
かな?
残念。違っているよ。
もう一度、「3分の1」と「2分の1」の大きさにを、図に書いて考えてみよう。
「3分の1」は、1を3コに分けた大きさだから、
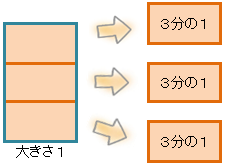
だね。
「2分の1」は、1を2コに分けた大きさだから、
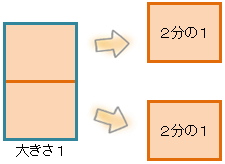
だね。
「3分の1」と「2分の1」を合わせて、1と比べてみると、下の図の大きさになるね。
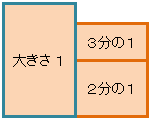
これに「5分の2」の大きさを並べてみると、こんな感じかな。
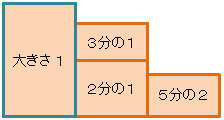
大きさが、全然違うね。
だから、
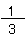 +
+  は
は 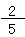 じゃないんだ。
じゃないんだ。
では、どうやって計算するんだろう。
分数の考え方を思い出してみよう。
「3分の1」は「三等分にしたときの1コ」だったよね。
「3分の1」が2つあると、「3分の2」になるよね。
これを式で書くと、
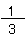 +
+ 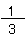 =
= 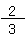
答えは合っているよ。さっきのたし算と何が違うんだろう?
そう、分母が同じ数なんだ。
分母は、1を「何等分にしたか」を表しているんだったよね。
「3分の1」は、3等分に分けているよね。「2分の1」は、2等分に分けているよね。
分けた数(分母)が違うから、たし算できないんだ。
いいかえると、たし算するためには、分母を同じ数にしないといけないんだ。
これは、大事なことを見つけたね。覚えておこう。
分数のたし算は、分母を同じ数にすればいいんだよね。
では、
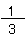 +
+ 
分数の考え方を思い出そう。
「3分の1」は、1を3コに分けた数だよね。(下の図の左から2番目だね。)
「3分の1」をほかの数で書き換えるには、全体をもっとたくさんの数に分ければいいんじゃないかな?
たとえば、全体を6等分したときはどうだろう?
6等分したときの図を書くと、こんな感じかな。(下の図の右から2番目だね。)
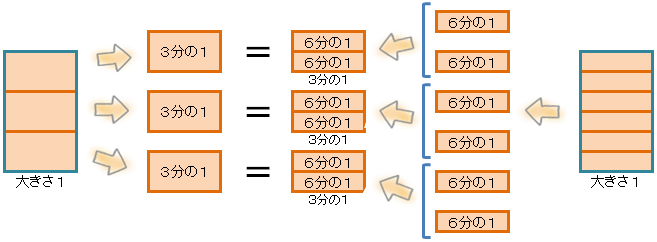
「3分の1」は「6分の2」に書きかえられたね。
ちなみに、3の倍数でない、4で分けたときの、図で書くと、こんな感じかな。

「4分の1」が4つを、余りがないように3つに分けられないから、「3分の1」は「4分の1」を使って書きかえられないね。
つまり、「3分の1」をほかの数で書き換えるには、全体を、3でちょうど割れて余りが無い数に、分ければいいんだ。
では「3でちょうど割れて、余りが無い数」はなんだろう?
そう、「3の倍数」で分ければいいよね。
「3の倍数」は、3でちょうど割れて、余りが無いよね。
さて、つぎに「2分の1」を考えよう。
さっきの「3分の1」と同じ考え方だね。
「2分の1」をほかの数で書き換えるには、全体を「2の倍数」で分ければいいんだ。
つまり、分母が「2の倍数」の分数で書きかえられるんだ。
たとえば、2の倍数の「4」でわけたときの、図を書くと、こんな感じかな。
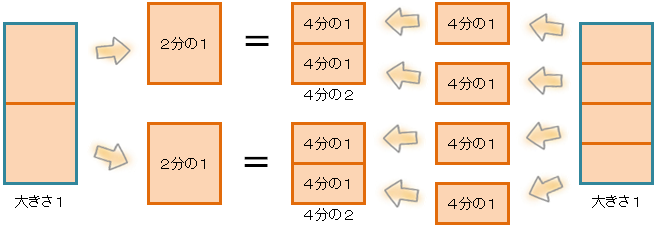
「2分の1」は「4分の2」に書きかえられたね。
さて、では、「3分の1」と「2分の1」をたし算するときの、分母の数はいくつかな?
「3分の1」は「3の倍数」でないと、書きかえられないし、「2分の1」は「2の倍数」でないと、書きかえられないよね。
ということは、分母は、「3の倍数であり、2の倍数でもある数」だったらいいよね。
「3の倍数であり、2の倍数でもある数」を「3と2の公倍数」っていうんだよね。
とくに、一番小さな公倍数を「最小公倍数」っていうんだったね。
「3と2の最小公倍数」は、「3分の1」と「2分の1」の両方を書きかえることができるから、
「3と2の最小公倍数」を使って、書きかえてみよう。
ところで、「3と2の最小公倍数」はいくつかな。
そう、「6」だよね。
では、
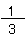 +
+ 
では、
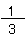 の分母を6に書きかえてみよう。
の分母を6に書きかえてみよう。分子も分母と同じ数をかけ算するんだったよね。
だから、
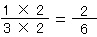
つぎに、
 の分母を6に書きかえてみよう。
の分母を6に書きかえてみよう。分子も分母と同じ数をかけ算するんだったよね。
だから、
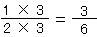
これで、分母を6にそろえられるね。
さぁ、式を書きかえよう。
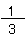 +
+  =
= 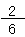 +
+ 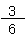
分数をたし算するときは、式を変形しよう。式が変形するなんて、おもしろいよね。
分数のたし算とひき算では、分母が同じときは、分母を一つにして、分子には、それぞれの分数の分子を書くんだ。
このとき、たし算のときは分子と分子のたし算に、ひき算のときは分子と分子のひき算に書きかえるんだ。
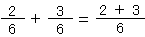
これを計算して、
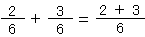
=
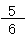
さて、問題は、
一人あたりが食べたリンゴは何個ですか?
その後、リンゴを3個買ってきて、6人で分けて食べました。
一人あたりが食べたリンゴは、さっき食べたリンゴと合わせて何個になりますか?
はじめの質問は
一人あたりが食べたリンゴは何個ですか?
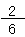 =
= 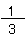
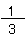 個
個次の質問は、
一人あたりが食べたリンゴは、さっき食べたリンゴと合わせて何個になりますか?
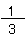 個を合わせて、
個を合わせて、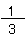 +
+ 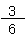 =
= 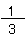 +
+ 
=
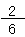 +
+ 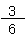
=
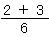
=
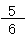
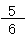 個
個分数のひき算
次の問題を考えてみよう。
切り分けた1コの大きさは、リンゴ1個の何コ分ですか?
つぎに、切り分けたリンゴを6人で1コずつ食べました。
残ったリンゴは、リンゴ1個の何コ分ですか?
さあ、考えよう。
はじめの質問は、
切り分けた1コの大きさは、リンゴ1個の何コ分ですか?
もとの数が、リンゴ2個で、それを8コに分けるから、式は、
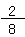
=
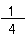
だから、答えは、
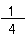 コ分
コ分
つぎの質問は、
残ったリンゴは、リンゴ1個の何コ分ですか?
質問は、はじめにリンゴが2個あって、何個か食べた後、残ったリンゴの個数を答えるんだよね。
食べた数が分かれば、ひき算すると、答えが分かるね。
そのときの式は、
では、食べたリンゴの数を計算しよう。
食べたリンゴの数は、
1コあたりの大きさは、さっき計算した
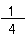 コだね。
コだね。食べた数は、問題文を読むと6人が一個ずつ食べたから、6コ食べたよね。
だから、食べたリンゴの数は、
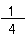 × 6
× 6=
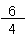
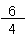 は約分できるよね。約分すると、
は約分できるよね。約分すると、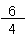
=
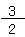
だから、残ったリンゴの数は、
= 2-
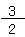
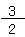
分数があるひき算だから、通分するといいね。
ここで、思い出してみよう。
 +
+  = 1
= 1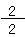 = 1
= 1では、2の場合はどうかな? 考えてみよう。
=
 +
+  +
+  +
+ 
 +
+  だからね。
だからね。これを、分母を残したまま計算すると、
 +
+  +
+  +
+ 
=
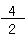
実は、分数を考えるときには、分母が1のときは、分母を省略できる(書かなくてもいい)んだ。
だから、
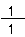
2 =
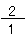
100 =
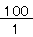
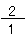
=
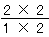
=
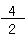
では、残ったリンゴの数を計算する式をもう一度考えよう。
残ったリンゴの数を計算する式は、
= 2-
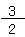
2を書きかえて通分すると、
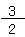
=
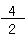 -
- 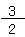
分数のたし算とひき算では、分母が同じときは、分母を一つにして、分子には、それぞれの分数の分子を書くんだ。
このとき、たし算のときは分子と分子のたし算に、ひき算のときは分子と分子のひき算に書きかえるんだ。
だから、
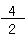 -
- 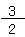
=
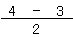
これを計算すると、
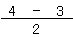
=

だから、答えは、
 コ分
コ分