ここでは、「分数」を説明するよ。
「分数」ってなぁに?
リンゴは、1コ、2コって数えるよね。では、下の問題を考えよう。
1コのリンゴを包丁(ほうちょう)でちょうど半分に切って、二つ(ふたつ)にしました。
半分に切ったリンゴ1つは、もとのリンゴのいくつ分の大きさでしょうか?
さて、どうやって考えよう。半分に切ったリンゴ1つは、もとのリンゴのいくつ分の大きさでしょうか?
まずは、図を描いてみよう。
1コのリンゴを、包丁で、半分にしたから、こんな感じかな。

半分のリンゴは2コになったね。
大きさを比べやすいように、リンゴを丸に描き替えよう。
こんな感じかな。分かりやすいように色も少し変えているよ。

では、半分に切ったリンゴ1つと、もとのリンゴの大きさを比べてみよう。
さっきの絵を重ね合わせるよ。

当然だけど、半分のリンゴ2コを合わせると、もとのリンゴ1コと同じ大きさだよね。
では、さっきの問題を考えてみよう。
半分のリンゴ1コは、もとのリンゴのどのくらいの大きさかな?
答えは、
答え)もとのリンゴをちょうど二つに分けたときの、1コ分の大きさ
だよね。「ちょうど二つに分ける」ことを、「ニ等分にする」っていうんだ。
これを使って言いかえると、答えは、
答え)もとのリンゴを、二等分にしたときの1コ分の大きさ
だね。算数では、「二等分にしたときの、1コ分」を、「2分の1」っていうんだ。
よみかたは「に ぶんの いち」だよ。
これを使って言いかえると、答えは、
答え)もとのリンゴの、2分の1の大きさ
だね。算数っぽい答えで、カッコいいね。
でも、もっとカッコいい書き方はないかな?
実は、「2分の1」を記号で書くことができるんだ。
「2分の1」を記号で書くと、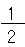 になるんだ。
になるんだ。
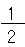 になるんだ。
になるんだ。このように書く数を「分数」って呼ぶんだ。
分数を書くときは、真ん中に線を引いて、下には「2分の1」の「2」を、上には「2分の1」の「1」を書くんだ。
図で書くとこんな感じかな。
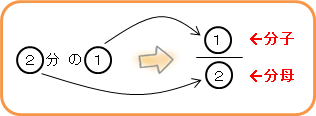
分数は上の数字と下の数字に読み方があるんだ。
上の数字を分子(ぶんし)、下の数字を分母(ぶんぼ)って呼ぶんだ。
ちなみに、真ん中の線を「括線」(かっせん)と呼ぶんだ。
「分数」ってなぁに?(2)
さっきは、リンゴで考えたけど、ここでは図を使って考えよう。
分数は、元の大きさを「1」として考えるんだ。
さっきのリンゴでは、リンゴ1コを「1」として考えたんだよ。
「1」とする大きさは何でもいいんだ。
下の図で、もとの四角形を「1」とするよ。
四角形を二等分したときの、1個の大きさを「2分の1」というんだ。
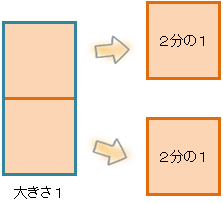
「○分の△」の、○には「1の大きさをいくつに分けたか」を書き、△には「分けたものをいくつ集めたか」を書くんだ。
式にするときは、「○分の△」の○を分数の分母に、△を分数の分子に書くんだ。
図で書くとこんな感じかな。

分数は上の数字と下の数字に読み方があるんだ。
上の数字を分子(ぶんし)、下の数字を分母(ぶんぼ)って呼ぶんだ。
ちなみに、真ん中の線を「括線」(かっせん)と呼ぶんだ。
四角形を四等分したときの、1個の大きさを「4分の1」といい、式で書くと、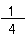 だ。
だ。
「4分の1」を2個合わせると、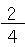 で、「2分の1」と同じ大きさになるんだ。
で、「2分の1」と同じ大きさになるんだ。
図で書くとこんな感じかな。
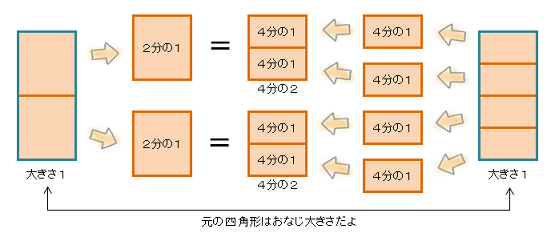
「分数」ってなぁに?(3)
では、分数を使ってみよう。
分数を使うことで、もっと分数のことが分かってくると思うよ。
下の問題を考えよう。
おおきな丸いケーキを、ナイフを使って、扇(おうぎ)型に四等分に切り分けました。
扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
さて、どうやって考えよう?扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
はじめに、図を書いて考えよう。
ケーキを、扇型に、四等分に、切り分けているから、図を書くとこんな感じかな。
ケーキは赤い丸で、点線がナイフで切ったところだよ。
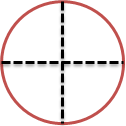
扇(おうぎ)型のケーキ1コは下のような形になるね。
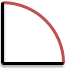
扇形(おうぎがた)ってどんな形?
「扇型」っていうのは、円の中心から引いた二本の線分(円の半径)と、その円の弧を結んでできる形をいうんだ。
たとえば、下の赤色の図形が、扇型だよ。

「扇型」っていうのは、円の中心から引いた二本の線分(円の半径)と、その円の弧を結んでできる形をいうんだ。
たとえば、下の赤色の図形が、扇型だよ。

さて、もとのケーキがいくつに分かれたかな?
そう、四つだよね。ケーキを「四等分」に切ったんだから、四つだよね。
扇型のケーキ1コは、「四等分にしたときの、1コ分」だから、
おおきな丸いケーキを、ナイフを使って、扇(おうぎ)型に四等分に切り分けました。
扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
の答えは、扇(おうぎ)型のケーキ1コは、もとのケーキの、何分の1の、大きさでしょうか?
答え)4分の1
だよね。式で書くと、
答え) 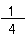
だね。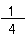
下の問題を考えよう。
おおきな丸いケーキを、ナイフを使って、扇(おうぎ)型に四等分に切り分けました。
扇(おうぎ)型の ケーキ2コ は、もとのケーキの、何分の1の、大きさでしょうか?
さっきの問題と似ているね。扇(おうぎ)型の ケーキ2コ は、もとのケーキの、何分の1の、大きさでしょうか?
ケーキを、扇型に、四等分に、切り分けているから、図を書くとこんな感じかな。
ケーキは赤い丸で、点線がナイフで切ったところだよ。

さっきの問題で答えたように、扇形のケーキ1コは、もとのケーキの4分の1の大きさだよね。
今回は、
扇形のケーキが2コだから「4等分に分けたときの2つ分」だから「4分の2」
だよね。「4分の2」でも間違っていないんだけど、小さな数を使って書き換えることができるんだ。
小さな数で書き換えると見やすくなるから、とても便利なんだ。
たとえば、「100000分の50000」よりは「2分の1」の方が見やすいでしょ。
では、どんな数で書き換えられるか考えよう。
ケーキを切った図に、4分の2を書き込んでみるよ。
赤い線が、4分の2だよ。
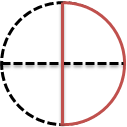
もしかして、ケーキの半分じゃないかな?!
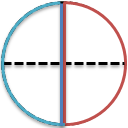
青い線で囲んだ扇型のケーキは4分の1が2コだから、4分の2の大きさだよね。
あ、赤い線と青い線は、同じ大きさだよね。
つまり、赤い線の大きさは、ケーキを、2等分したときの1コ分、と同じ大きさだよね。
いいかえると、赤い線の大きさは、もとのケーキの2分の1の大きさだよね。
あれ? さっき答えは「4分の2」だったけど「2分の1」になったね。
間違いじゃないよ。
「4分の2」と「2分の1」は同じ大きさなんだ。
だから、「4分の2」は「2分の1」に書き換えていいんだ。
小さな数で書き換えるために、毎回、図を書くのは大変だよね。
記号を使って計算する方法を考えてみよう。
はじめに、ケーキを2等分にしてみよう。
次にケーキを4等分にした大きさを考えて、最後にケーキを8等分した大きさを考えてみよう。
はじめは、2等分するよ。
図の赤い図形は、全体を2等分したうちの1つだよ。
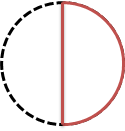
おおきさは、「2分の1」だよね。
つぎに、全体を4等分にしてみよう。
全体は4コに分かれるね。
青い図形が「4分の1」だね。
ちなみに、赤い図形は「2分の1」だったね。
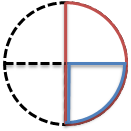
図からもわかるように、青い図形の2個分と、赤い図形が同じ大きさだよね。
青い図形は「4分の1」だから、その2個分は「4分の2」だよね。
つまり、「4分の2」は「2分の1」に書きかえることができるんだね。
つぎに、全体を8等分にしてみよう。
全体は8コに分かれるね。
緑の図形が「8分の1」だね。
ちなみに、青い図形が「4分の1」で、赤い図形が「2分の1」だったね。
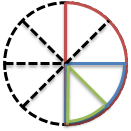
図からもわかるように、緑の図形の2個分と、青い図形が同じ大きさだよね。
緑の図形は「8分の1」だから、その2個分は「8分の2」だよね。
つまり、「8分の2」は「4分の1」に書きかえることができるんだね。
そしてもう一つ、図からわかるように、緑の図形の4個分と、赤い図形が同じ大きさだよね。
緑の図形は「8分の1」だから、その4個分は「8分の4」だよね。
つまり、「8分の4」は「2分の1」に書きかえることができるんだね。
全体を4等分したとき、「4分の2」は「2分の1」に書きかえることができたから、
全部まとめると、「8分の4」=「4分の2」=「2分の1」なんだね。
さて、下に書きかえた数を、まとめてみたよ。
・4分の2 = 2分の1
・8分の4 = 4分の2
= 2分の1
分かったことを文章で書くと、・8分の4 = 4分の2
= 2分の1
「2分の1」と「4分の2」と「8分の4」は同じ大きさで、「2分の1」の大きさ。
だね。もう、気が付いたかな。
「○分の△」の○と△を、同じ数でわり算したときや、同じ数をかけ算したときは、もとの数の大きさと変わらないんだ。
たとえば、
「2分の1」の「2」と「1」を2倍にすると「4分の2」になるよね。
「4分の2」は「2分の1」と同じだったよね。
たとえば、「4分の2」は「2分の1」と同じだったよね。
「2分の1」の「2」と「1」を4倍にすると「8分の4」になるよね。
「8分の4」は「2分の1」と同じだったよね。
お。「○分の△」の○と△に同じ数(2や4)をかけ算しても、大きさは変わらないね。「8分の4」は「2分の1」と同じだったよね。
次は、わり算してみよう。
たとえば、
「4分の2」の「4」と「2」を、2で割ると、「2分の1」になるよね。
たとえば、
「8分の4」の「8」と「4」を、4で割ると、「2分の1」になるよね。
お。「○分の△」の○と△を同じ数(2や4)で割っても、大きさは変わらないね。「○分の△」の○と△を、同じ数でわり算したときや、同じ数をかけ算したときは、もとの数の大きさと変わらないことは大事なことだから覚えよう。
分数の記号で考えてみよう。
・2分の1は、
・4分の2は、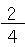 =
=
・8分の4は、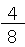 =
=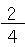
=

・4分の2は、
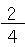 =
=
・8分の4は、
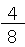 =
=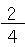
=

もう、気が付いたかな。
分母と分子を、同じ数でわり算しても、かけ算しても、大きさは同じになっているね。
たとえば、
 の分母「2」と分子「1」をそれぞれ2倍にすると、
の分母「2」と分子「1」をそれぞれ2倍にすると、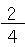 になるよね。
になるよね。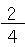 =
= 、だったよね。
、だったよね。 の分母「2」と分子「1」をそれぞれ4倍にすると、
の分母「2」と分子「1」をそれぞれ4倍にすると、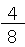 になるよね。
になるよね。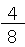 =
= 、だったよね。
、だったよね。次は、わり算してみよう。
たとえば、
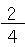 の分母「4」と分子「2」を、それぞれ2で割ると、
の分母「4」と分子「2」を、それぞれ2で割ると、 になるよね。
になるよね。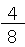 の分母「8」と分子「4」を、それぞれ4で割ると、
の分母「8」と分子「4」を、それぞれ4で割ると、 になるよね。
になるよね。
緑のおおぎ型は「8分の1」だったね。その4個分は「8分の4」で、赤色の扇型と同じ大きさだね。
赤色のおおぎ型は「2分の1」だったから、「8分の4」と「2分の1」は同じ大きさだったね。
分母と分子を、同じ数でわり算しても、かけ算しても、数の大きさは変わらないことは大事なことだから、おぼえておこう。
ちなみに、分母と分子を、同じ数でわり算することを約分(やくぶん)というんだ。
「約分」って言い方はカッコいいよね。忘れずにおぼえておこう。