ここでは、「小数」を説明するよ。
「小数」ってなぁに？
距離（きょり）はメートル（ｍ）やキロメートル（ｋｍ）を使って表すよね。たとえば、100ｍ、500ｍ、って書くよね。
距離がもっと長くなると、10,000ｍや50,000ｍ、って書くよね。
10,000ｍや50,000ｍって、数字がたくさん並んで、パッと見た時に分かりにくいよね。
だから、「単位」を変えて、パッと見た時にわかりやすくするんだ。
「単位」ってなにかって？
単位は数字の後につける言葉や記号なんだ。
単位が変わると数字の大きさや意味が変わるから、単位はとても重要なんだ。
このときの単位は、量を表す「コ」だ。
このときの単位は、長さを表す「ｍ（メートル）」だ。
このときの単位は、重さを表す「ｋｇ（キログラム）」だ。
では、10,000ｍを分かりやすくするために、単位をｍ（メートル）からｋｍ（キロメートル）に変えてみよう。
1,000ｍ＝1ｋｍなんだ。だから、
50,000ｍ＝50ｋｍ
並んでいる数字が少なくなって見やすくなるよね。
ところで、「10,500ｍ」は何ｋｍだろう？
さっきの「10,000ｍ」と違うところは、「500ｍ」があるのが違うよね。
10,000ｍは10ｋｍだったよね。
だから「10,500ｍ」は「10ｋｍと500ｍ」かな？
実は、数には「小数」っていうのがあるんだ。
１ｋｍと２ｋｍの差は「１」ｋｍだよね。
その「１」を１０等分にしたとき、その１コ分を「0.1」（れー てん いち）と書くんだ。
式で書くと、
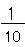＝ 0.1なんだ。
0.1の次は0.2、0.3と増えていくよ。0.9の次は1だよ。
図を書くとこんな感じかな。
小数はどこでも使えるよ。たとえば、０から２までを書くとこんな感じかな。
「1.1」や「1.2」の「.」（てん）は、「小数点」というんだ。
そして、「1.1」や「1.2」のように、「小数点」がある数を「小数」というんだ。
さて、さっきの、
100ｍは、「1,000ｍの１０分の１」だよね。
ということは、
100ｍは、「１ｋｍの１０分の１」だよね。
ということは、
100ｍは、「0.1ｋｍ」になるよね。
500ｍは100ｍの5倍だから、
500ｍは、「0.1×5ｋｍ」＝「0.5ｋｍ」だよね。
では、
つまり、10,500ｍは10,000ｍと500ｍを足した長さだよね。
「10,000ｍ＝10ｋｍ」、「500ｍ＝0.5ｋｍ」だから、
つぎの問題を考えてみよう
1メートルは、100ｃｍだよね。
だから、２.５６ｍの中の、２ｍは２００ｃｍだよね。
残りの、０.５６ｍの中の、０.５ｍは、何ｃｍだろう？
０.１ｍは、１ｍの１０分の１だよね。
順をおって考えてみると、
＝５０ｃｍ
残りの、０.０６ｍは、何ｃｍだろう？
もっとカッコよく計算できないかな？
「ｃｍ」の単位で考えると、
２.５６ｍは、１００ｃｍが２.５６コある、ってことだよね。
カッコよく計算できたね。
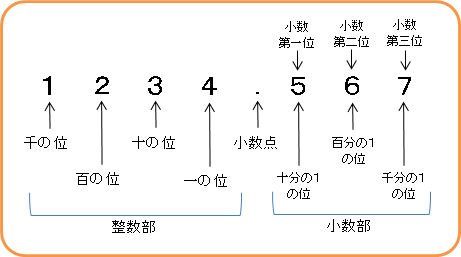
小数には、桁によって呼び方があるんだ。
小数では、小数点の左を整数部、右を小数部っていうんだ。
たとえば、「２．５６」の整数部は「２」だね。
小数点のすぐ右の桁を、小数第一位というんだ。
「２．５６」の小数第一位は「５」だね。
小数第一位は、１０分の１の大きさなんだ。
小数第一位の右の桁を、小数第二位、その次を小数第三位っていうように続くんだ。
「２．５６」の小数第二位は「６」だね。
小数第二位は、小数第一位の１０分の１の大きさなんだ。
言い換えると、小数第二位は、１００分の１の大きさなんだ。
「小数」のたし算
小数をたし算するときは、桁を合わせてたし算するんだ。
計算のやり方は、整数と整数のたし算のひっ算と同じで、同じ桁の数を一番小さな桁から順に足すんだ。
小数部は、小数第二位と小数第二位を、小数第一位と小数第一位を、たし算するんだ。
整数部は、一の位と一の位を、十の位と十の位を、たし算するんだ。
では次の問題を考えよう。
小数第一位を足すと「１＋１＝２」、一の位を足すと「１＋０＝１」だね。
だから答えは、
式）
１．１＋０．１＝１．２
答え）
１．２
小数のたし算もひっ算で計算することができるよ。
計算するときは、整数と整数のたし算と同じように、桁ごとに計算するんだ。
桁を合わせるには、小数点の位置を合わせたらいいよね。忘れないように注意しよう。
たとえば、「１．１」に「０．１」を足すときは、小数点の位置を合わせて、
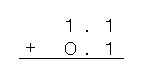
のように書くんだ。
これを計算すると、
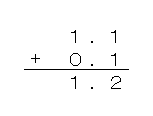
になるね。
何度も言うけど、小数点の位置を合わせることに注意しよう。
では次の問題を考えよう。
小数のひっ算は小数点の位置を合わせて書くんだよね。
だから、
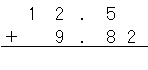
だね。
計算のやり方は、整数と整数のたし算のひっ算と同じで、同じ桁の数を一番小さな桁から順に足すんだ。
はじめに、小数第二位を足すんだ。。。あれ？、２の上に数字がないね。
このときは「０」と考えるんだ。１２．５と１２．５０は同じ大きさの数でしょ。
だから、小数第二位を計算すると、
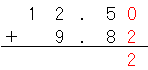
だね。
次に小数第一位を計算すると、
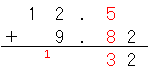
だね。くり上がりに注意しよう。
小数第一位の繰り上がった数は一の位になるよ。「０．１」が十個集まると「１」になるからね。
繰り上がりの数の書き方はいろいろあるよ。
ひっ算を使うの理由は、計算間違えしないで速く計算するためだよ。
繰り上がりの書き方を気にするよりも、計算間違えしないで速く計算できるように練習しよう。
そのためにも、ひっ算の書き方はどれか一つに決めて、毎日計算の練習をしよう。
考え方があっているのに、計算間違いで不正解だと、悲しくなるからね。
次に一の位を計算すると、
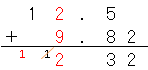
だね。くり上がった１を足すのを忘れないようにしよう。
くり上がりもしているから忘れないように注意しよう。
次に十の位を計算すると、
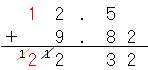
だね。
だから答えは、、、ちょっとまって。
大事なことを忘れているよ。小数点はどうすればいいの？
そうだね。一の位と小数第一位の間に書かないとといけないよね。
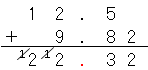
だから答えは、
式）
１２．５＋９．８２＝２２．３２
答え）
２２．３２
「小数」のひき算
小数をひき算するときは、桁を合わせてひき算するんだ。
計算のやり方は今までの整数と整数のひき算と同じだよ。小さな位から計算するんだ。
小数部は、小数第二位と小数第二位を、小数第一位と小数第一位を、ひき算するんだ。
整数部は、一の位と一の位を、十の位と十の位を、ひき算するんだ。
では次の問題を考えよう。
小数第一位を引くと足すと「３－１＝２」、一の位を引くと「４－１＝３」だね。
だから答えは、
式）
４．３－１．１＝３．２
答え）
３．２
小数のひき算もひっ算で計算することができるよ。
計算するときは、整数と整数のひき算と同じように、桁ごとに計算するんだ。
桁を合わせるには、小数点の位置を合わせたらいいよね。忘れないように注意しよう。
たとえば、「４．３」から「１．１」を引くときは、小数点の位置を合わせて、
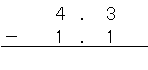
のように書くんだ。
これを計算すると、
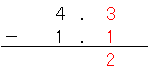
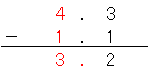
になるね。
何度も言うけど、小数点の位置を合わせることに注意しよう。
では次の問題を考えよう。
小数のひっ算は小数点の位置を合わせて書くんだよね。
だから、
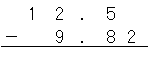
だね。
計算のやり方は整数と整数のひき算のひっ算と同じで、同じ桁の数を一番小さな桁から順に引くんだ。
はじめに、小数第二位を引くんだ。。。あれ？、２の上に数字がないね。
たし算で考えたのと同じように、このときは「０」と考えるんだ。１２．５と１２．５０は同じ大きさの数でしょ。
書きかえると、
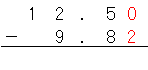
だね。
０から２は引けないから、小数第一位から１を引いて、小数第二位を計算すると、
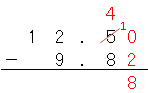
だね。
繰り下がりの数の書き方はいろいろあるよ。
ひっ算を使うの理由は、計算間違えしないで速く計算するためだよ。
繰り下がりの書き方を気にするよりも、計算間違えしないで速く計算できるように練習しよう。
そのためにも、ひっ算の書き方はどれか一つに決めて、毎日計算の練習をしよう。
考え方があっているのに、計算間違いで不正解だと、悲しくなるからね。
次に小数第一位を計算すると、
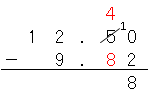
４から８は引けないから、一の位から１を引いて、小数第一位を計算すると、
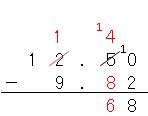
だね。
次に一の位を計算すると、
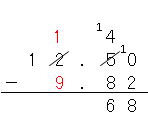
１から９は引けないから、十の位から１を引いて、一の位を計算すると、
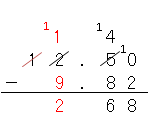
だね。
だから答えは、、、ちょっとまって。
大事なことを忘れているよ。小数点はどうすればいいの？
そうだね。一の位と小数第一位の間に書かないとといけないよね。
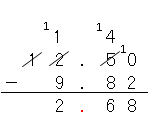
だから答えは、
式）
１２．５－９．８２＝２．６８
答え）
２．６８
