ここでは、速さについてもっと考えよう。
船の速さを考えよう
「距離・速さ」では、車や自転車、歩く速さを考えたね。
ここでは、船の速さを考えてみよう。
船の速さは、車や自転車の速さと同じなんだろうか?
次の問題を考えてみよう。
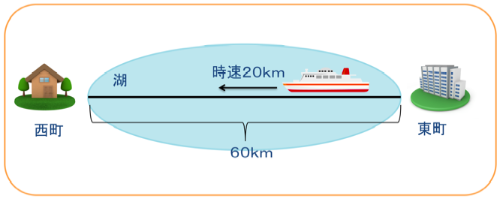
フェリーで行くと、東町から西町までの距離は60kmです。
フェリーは時速20kmの速さで水の上を進みます。
東町から西町までフェリーで行くのに何分かかりますか。
今日は風も吹いておらず、湖は穏やかで水の流れもありません。
まずは図を書いてみよう。
図を書くとこんな感じかな。
ところで、移動にかかる時間は、どうやって計算するか覚えているかな?
例えば、自転車に乗って、近くの公園に行く場合と、その2倍の距離はなれた小学校に行く場合を考えると、
小学校に行くほうが時間がかるよね。だって、遠いのだから。
つまり、
では、次に移動する速さが変わると、移動にかかる時間はどうなるか考えよう。
日本の横浜から、オーストラリアのシドニーまでは、どこにも寄り道せずに移動するなら、船と飛行機ではどっちが早く着くかな。
もちろん飛行機だね。飛行機のほうが速いからね。
つまり、
まとめると、
2)「移動する速さ」が「速くなる」と、「移動にかかる時間」は「短くなる」
上のどちらの文章にも「移動にかかる時間」が含まれているね。だから「移動にかかる時間」を計算する式を考えてみよう。
「比例」と「反比例」で考えると、
2)「移動にかかる時間」は「移動する速さ」に反比例する
だから、式を書くと、
これで移動にかかる時間を計算することができるね。
■比例
「移動する距離」が「2倍」に「増える」と、「移動にかかる時間」も「2倍」に「増える」よね。
「移動する距離」が「10倍」に「増える」と、「移動にかかる時間」も「10倍」に「増える」よね。
このように、一方が増えたときに、もう一方も同じだけ増える関係を「比例」っていうんだ。
文章で書くと、「移動にかかる時間 は 移動する距離 に 比例する」って書けるんだ。
■反比例
「反比例」は「比例」に「反」がついているね。「反」がついているだけあって、「比例」の逆の意味なんだ。
「移動する速さ」が「2倍」に「増える」と、「移動にかかる時間」は「2分の1」に「減る」よね。
「移動する速さ」が「10倍」に「増える」と、「移動にかかる時間」は「10分の1」に「減る」よね。
このように、一方が増えたときに、もう一方も同じだけ減る関係を「反比例」っていうんだ。
文章で書くと、「移動にかかる時間 は 移動する速さ に 反比例する」って書けるんだ。
移動にかかる時間は、
フェリーで移動する距離は60km、フェリーで移動する速さは時速20kmだから、式に当てはめると、
= 3
答え)
移動にかかる時間は、3時間
時間はあっているんだけど、答え方がちょっと違うね。
問題文には、「何分かかりますか」って書いているね。
だから、時間の単位を計算し直そう。
1時間は、60分だね。
3時間は、何分かな?
3時間 = ?分
だって、=は左側と右側が同じ値ってことなんだから、左側に3をかけた値と、右側に3をかけた値は同じ値になるよね。
1時間×3 = 60分×3
1×3時間 = 60×3分
3時間 = 180分
だから答えは、
移動にかかる時間は、180分
水の流れがあるときの船の速さ
では次に、海をフェリーで進むときの時間を計算してみよう。
海には、海流があって、水が流れている場所があるよね。
日本の近くでは、対馬海流や黒潮海流って読んでいる海流があるんだ。
では、次に海流のように水の流れがある場所をフェリーで進むときの速さを考えてみよう。
次の問題を考えてみよう。
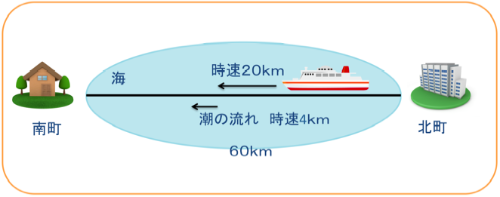
フェリーで行くと、北町から南町までの距離は60kmです。
フェリーは時速20kmの速さで水の上を進みます。
北町から南町までフェリーで行くのに何分かかりますか。
風は吹いておらず海は穏やかですが、北町から南町に向かって、時速4kmの潮の流れがあります。
まずは図を書いてみよう。
図を書くとこんな感じかな。
移動にかかる時間は、
フェリーで移動する距離は、北町から南町までの距離だから、60kmだね。
フェリーで移動する速さは、時速20kmだよね?
だから式は、
= 60 ÷ 20
= 3
あれ? 水の流れは考えなくていいのかな?
みんなは流れるプールで泳いだことあるかな?
浮き輪でプカプカ浮かんでいるだけなのに、水の流れに乗って進むよね。
実はフェリーも同じなんだ。
フェリーは水の上に浮かんでいるから、水が動くとフェリーも動くんだ。
フェリーがエンジンをかけずに海に浮かんでいるときは、どのくらいの速さで進むのかな?
フェリーは水の上に浮かんでいるから、水が動いた距離だけフェリーも動くね。
はじめに、北町にフェリーが停まっているときを図で書くとこんな感じかな。
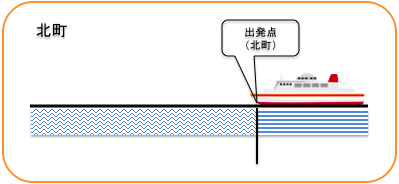
水の流れは時速4kmだから、水は1時間で4km進むよね。だからフェリーも1時間で4km進むんだ。
図を書くとこんな感じかな。
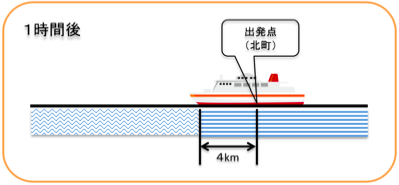
また、フェリーはエンジンをかけると水の上を時速20kmですすむから、1時間後には水に対して元の位置から20km進むよね。
図を書くとこんな感じかな。
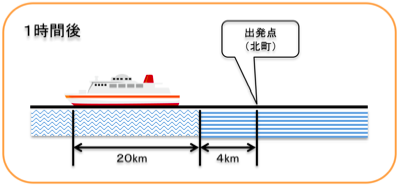
では、実際にフェリーの進む速さを考えてみよう。
1時間でフェリーが進む距離は、水がフェリーを動かした距離と、フェリーが水の上を進んだ距離の和だから、
= 4 + 20
= 24
だから、
フェリーが北町から南町に向かって進む速さは、時速24km。
これを使って、式を書くと、
= 60 ÷ 24
= 2.5
移動にかかる時間は、2.5時間。
時間の単位を分に書き換えると、
2.5時間 = 60×2.5分
= 150分
移動にかかる時間は、150分
さっきの問題では水の流れがない場合を考えたけど、水の流れがある方が、水の流れがないときより、早く着くんだね。
では次に、南町から北町に行くときはどのくらいの時間がかかるか考えてみよう。
次の問題を考えよう。
フェリーで行くと、南町から北町までの距離は60kmです。
フェリーは時速20kmの速さで水の上を進みます。
南町から北町までフェリーで行くのに何分かかりますか。
風は吹いておらず海は穏やかですが、北町から南町に向かって、時速4kmの潮の流れがあります。
水の流れはフェリーの進む方向と逆向きだから注意しよう。
ここから先は工事中。
距離・速さを考えよう(2)の説明はここでおわりだよ。