ここでは、負の数の加算・減算を学ぼう。

負の数ってなに？

これまでは、正の数を考えてきたけど、ここでは負の数を考えよう。
正の数というのは、０より大きい数なんだ。
たとえば、１，２，３、だね。
負の数は０より小さい数なんだ。
０より１だけ小さい数を「-１」、０より２だけ小さい数を「-２」と書くんだ。
０より４だけ小さい数は「-４」になるよ。「-」は「マイナス」って読むよ。
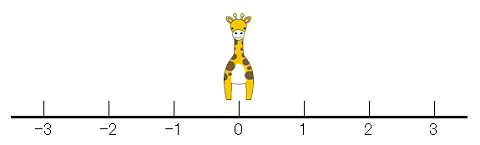
図で書くとこんな感じかな。

これまでは、「Ａさんはリンゴを８個持っている。」というように正の数を考えてきたね。
では、負の数はどんな時に使うんだろう？

リンゴが-１個、リンゴが-２個とは言わないのかな？
実はこれまでも負の数を使っているんだ。
「Ｂさんの持っているリンゴはＡさんのリンゴの数より２個少ない。」というよね。
これを負の数を使って書くと「Ｂさんの持っているリンゴの数は、Ａさんのリンゴの数-２個」となるんだ。
「-２」っていう負の数が出てきたね。
正の数は、元の数に比べて、１大きい時を１、２大きい時を２と考えているんだけど、
負の数は、元の数に比べて、１小さい時を-１、２小さい時を-２と考えているんだ。

「Ｂさんの持っているリンゴはＡさんのリンゴの数-２個」のとき、
「Ａさんはリンゴを８個持っている」とすると、Ｂさんはその-２個だから、何個のリンゴを持っているかな。
そうだね、式を書くと、

となるんだ。これを計算すると、
だから、リンゴを６個持っているんだね。

では、次の場合は、Ｂさんの持っているリンゴはＡさんの持っているリンゴより何個多い（または少ない）かな？

これを式にすると、1) のときはＢさんの持っているリンゴとＡさんの持っているリンゴの数は同じだから、
だね。次に2)はＢさんの持っているリンゴが２個増（ふ）えたから、
だから、差は２個になるね。
つぎに3)はＢさんのリンゴが３個減ったから、
だね。これを計算すると
だね。だから3)のときはＢさんの持っているリンゴの数は、Ａさんの持っているリンゴの数よりも１個少ないんだね。
負の数を使うと、元の数からどのくらい変わったかがわかるから便利だね。

負の数のたし算（加算）

負の数の加算はどうやってするか考えよう。
次の計算を考えよう。

さあ考えよう。
足し算だから、「＋」の記号を使うんだよね。
かな？。
記号が続いて書かれているから見づらいよね。
こういう時はカッコを使って書くんだ。
見やすくなったね。３と（－５）を足すことがわかりやすいね。
負の数を書くときはカッコでくくろう。

では、計算してみよう。
３と（－５）を足すと・・・負の数を足すってどういうことだろう？

負の数は元の数からどれだけ減っているかの数なんだ。
だから、負の数は引き算になるんだ。

さっきの式

を計算しよう。
負の足し算は引き算に書き換えられるから、
だね。これを計算して、
だね。

次に別の考え方で下の式を考えてみよう。

はじめに、３という数は、０に３を足した数だよね。
式で書くと、
になるね。式全体を書き換えると、
だね。はじめの０は、数直線の０の位置に立っている、と考えよう。
図で描くとこんな感じかな。



式の続きを考えよう。次は＋３だね。式でいうと、
のところだね。
足し算になっているね。
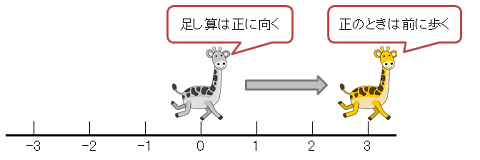
足し算は増える方向だよね。だから「増える方向」＝「正の方向」に向かって立っていると考えよう。
そして、足す数は、３よだね。だから、前に３つ進もう。
図で描くとこんな感じかな。



３の位置に来たね。ここまでで、
を考えたね。
式の続きを考えよう。つぎは３から後ろの式だね。
はじめに足し算になっているから、さっきと同じように「増える方向」＝「正の方向」に向かって立っていると考えよう。
そして、足す数は負の数「－５」だね。
初めに見た数直線をもう一度見てみよう。負の数は正の数とは逆の方向だよね。

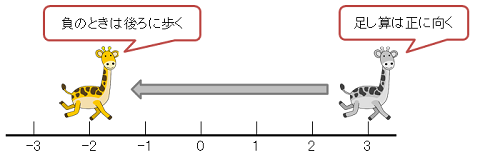
だから、前に進むのではなくて、後ろに進もう。
（－５）だから後ろ向きに５つ進もう。
図で描くとこんな感じかな。



さぁ今いる位置はどこかな？
（－２）だね。だから、さっきの式の答えは、
だね。同じ答えになったね。

負の数のひき算（減算）

ここでは、負の数の引き算を考えよう。
では次の式を考えよう。

負の数を引くってどういうことだろう？

さっきの式を考える前に、下の式を考えよう。

はじめの３を考えると、
今は３に立っていよるね。図で描くとこんな感じかな。



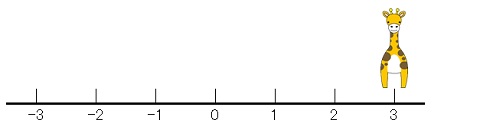
つぎは３から後ろの式だね。
引き算だから、値が減るんだよね。だから、「値が減る方向」＝「負の方向」に向かって立っているんだよね。
そして、引く数は正の数「５」だから、前に５つ進むよね。
図で描くとこんな感じかな。



さぁ今いる位置はどこかな？
（－２）だね。だから、さっきの式の答えは、
だね。

では、はじめの式を考えよう。
式は、

だったね。
はじめの３を考えると、
今は３に立っているよね。図で描くとこんな感じかな。



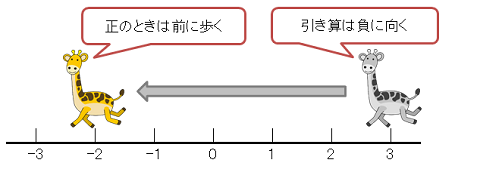
つぎは３から後ろの式だね。
引き算だから「値の減る方向」＝「負の方向」に向かって立っているよね。
そして、引く数は負の数（－５）だから、後ろ向きに５つ進もう。
図で描くとこんな感じかな。



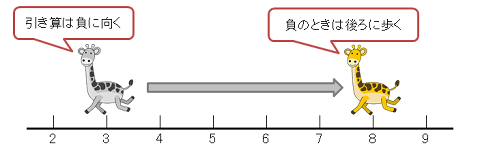
さぁ今いる位置はどこかな？
８だね。だから、さっきの式の答えは、
だね。

負の値を引くと元の値から増えているよね。
ひき算なのに、値が増えるのはおかしい？
さっきの式は３から（－５）を引いたら８になったね。値が増えているね。

大きな値を引くと値が大きく減るよね。小さな値を引くと値は少ししか減らないよね。
たとえば、ある数から１０００を引くと１０００減るし、ある数から１０引くと１０減るよね。
じゃあ、ある数から０を引くといくつ減るかな？　そう、値は減らないよね。
じゃあ、ある数から（－１０）引くとどうなるかな？
（－１０）は０より小さい数だよね。０のときは減らないから、（－１０）は逆に増えるんだよ。
数直線を思い出そう。
負の数（－）は正の数（＋）とは０を中心として逆向きなんだ。
だから、正の数を引くと値が減るけれど、負の数を引くと値が増えるんだ。
「１０円玉の裏の裏は表」と同じ？

「３－（－５）」を計算するときに、毎回図を描いていると大変だよね。
もっとカッコよく計算できないかな。

「－（－５）」を計算するときは、数直線を負の方向を向いて後ろに進んだね。
これは、数直線を正の方向に向いて前に進むのと同じだよね。
つまり、負の数の引き算は、正の数の足し算に書きかえられるってことだよね。
もとの式を書き換えると、

だね。
これを計算すると、
だね。
負の数の引き算は、正の数の足し算に書きかえられるんだね。覚えておこう。

では、次の式を計算してみよう。

むつかしそうだけど、これまで学んだことを思い出そう。
足し算や引き算よりも、先にカッコの中を計算するんだったよね。
だね。
負の数の引き算だから、正の数の足し算に書きかえられるよね。
さっきと同じように書きかえると、
だから答えは、
だね。

さっきはカッコの中を先に計算したけど、カッコを外してから計算することもできるよ。

それではカッコを外してみよう。

カッコの最初の数は（－５）だね。これは負の数の引き算だね。

だから、正の数の足し算に書きかえられるね。

カッコの次の数は＋２だね。これは正の数の引き算だね。

だから、正の数の引き算に書きかえられるね。
両方を書きかえると、
だね。これを計算すると、
になるね。
カッコの中を先に計算したときと同じ答えになったね。