ここでは、３つ以上の数の「公倍数（こうばいすう）」と「公約数（こうやくすう）」について考えよう。

３つ以上の数の公倍数と最小公倍数

公倍数を考えるときには、素因数分解を使って計算したよね。
２つの数の最小公倍数は「公倍数・公約数の計算」の「最小公倍数を計算する」で計算したね。
３つ以上の数のときも、同じ考え方で計算すればいいんだ。

次の問題を考えよう。

さあ、考えよう。

この問題をカッコよく答えるには、２と３と４の最小公倍数を考えればいいよね。
なぜなら、最小公倍数の倍数が、２と３と４の公倍数になるんだったよね。

最小公倍数を計算するには、２と３と４を素因数分解して、最小公倍数がそれらの素因数を含んでいればいいんだよね。

「２」は素数だね。
だから、最小公倍数には「２」を含んでなければならないよね。

「３」は素数だね。
だから、最小公倍数には「３」を含んでなければならないよね。

「４」は素因数分解すると、「２×２」だね。
だから、最小公倍数には「２×２」を含んでなければならないよね。

上の３つをまとめると、最小公倍数は「２×３×２」になるから、最小公倍数は「１２」だね。

答えは最小公倍数である１２の倍数になるから、

だね。

３つ以上の数の公約数と最大公約数

公約数を考えるときには、素因数分解を使って計算したよね。
２つの数の最大公約数は「公倍数・公約数の計算」の「公約数と最大公約数を計算する」で計算したね。
３つ以上の数のときも、同じ考え方で計算すればいいんだ。

次の問題を考えよう。

さあ、考えよう。

この問題をカッコよく答えるには、まずは公約数を計算して、公約数の中で一番大きな数、つまり、最大公約数を計算すればいいよね。
公約数を考えるには、２４と３２と３６をそれぞれ素因数分解して、いずれの数にも含まれている素因数を書き出していけばいいよね。

「２４」を素因数分解すると「２×２×２×３」だね。
「３２」を素因数分解すると「２×２×２×２×２」だね。
「３６」を素因数分解すると「２×２×３×３」だね。
いずれの数にも含まれている素因数は、２が二つだね。

だから公約数は、１と、二つの２を使ってできる数だね。
公約数は小さい順に、

の３つだね。
最大公約数は、公約数で一番大きな数だから「４」だね。
だから、答えは、
だね。

最大公約数をひっ算で計算してみよう。

次の問題を考えよう。

次はひっ算で計算してみよう。

素因数分解のひっ算と同じように計算するよ。
ただし、公約数を計算する数字を横に並べるんだ。

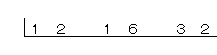
つぎに、並べた全部の数が、割り切れる数で素因数分解していくんだ。
割り切れる数を探すときは、小さな数から考えていくと計算しやすいね。
２で割り切れるかな？．．．１２と１６と３２は２で割り切れるね。
だから、

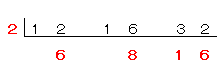
になるね。
次はどうだろう？
また、２で割り切れるかな？．．．６と８と１６は２で割り切れるね。
だから、

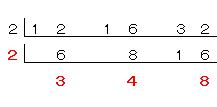
になるね。
次はどうだろう？
３と４と８を割り切れる数はあるかな？
そう、もうこれ以上は素因数分解できないね。

最大公約数は、ひっ算の左側にある数（下の赤色の数）、をかけ算した数なんだ。

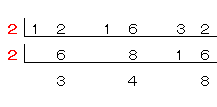
最大公約数は、２×２＝４、だ。
だから、答えは、

ちなみに、左側の数を組み合わせてかけ算した数が、公約数になるよ。
１２と１６と３２の公約数は、１と２を二つ組み合わせてできる数だから、
の三つだね。
「１」はひっ算には含まれていないけど、公約数だから忘れずに書こう。